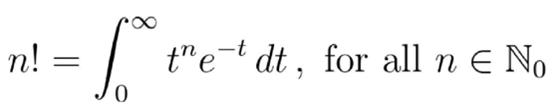
文章图片

这就是欧拉的定义 。 要证明这个积分等于阶乘 ， 我们把右侧的积分叫做Π(n) ， 然后分部积分：

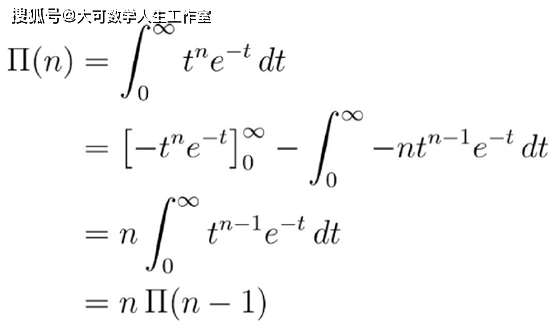
文章图片

利用这个函数方程 ， 我们就可以用归纳法来证明上面的公式 。 我们想要证明Π(n)=n！对任何自然数n成立 。 首先 ， 注意：

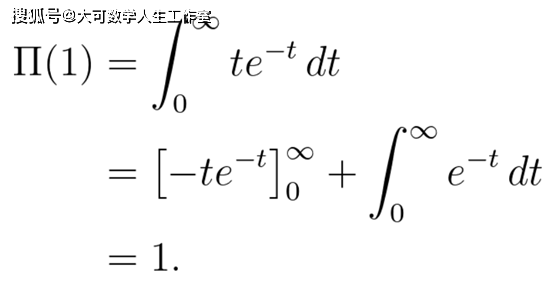
文章图片

即 ， Π(1)=1!
然后 ， 假设Π(n-1)=(n-1)! ， 那么我们有 Π(n)=nΠ(n-1) =n(n-1)!=n!
这里用到了上面的函数方程 。 根据归纳法 ， 命题得证 。 注意 ， 上面关于Π(n)的定义 ， n并不一定是自然数 。 这个表达式对所有实部为正的复数都是讲得通的 。
处理广义阶乘的现代方法就是Gamma函数 。 Gamma函数与刚刚的Π函数十分相似 ， 定义如下：

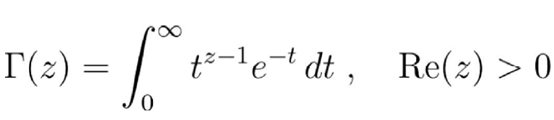
文章图片

注意：对任何自然数n ， 有Γ(n)=Π(n-1)=(n-1)! 。 因此 ， Gamma函数也满足一个相似的函数方程：Γ(z+1)= zΓ(z) 。
所以Gamma函数是广义的阶乘函数 ， 因为对所有的非负整数n ， 有Γ(n+1)= n! 。
【这可能是世上最美丽的函数】但这是推广Gamma函数的唯一方式吗？
不幸的是 ， 答案是否定的 。 然而 ， 如果我们添加某种约束的话 ， 它就是唯一的了 。 这个约束与对数凸性(logarithmic convexity)这个概念有关 ， 因为稍微有点偏题 ， 在这里就不详细讲了 。 具体的要求是函数logΓ是凸的 。
★
TIP
★
一个二次可微的函数f是对数凸的 ， 当且仅当

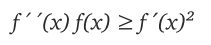
文章图片

重要的是 ， 如果你想推广阶乘 ， Gamma函数在特定的数学意义上是一个十分自然的选择 。
Weierstrass积
Gamma函数的定义和形式数不胜数 。 一个尤其nice的是一种无穷乘积 。 在此之前 ， 我们试试从我们的定义中推出一些有趣的结果吧 。
我们要做的第一件事可能看起来有些奇怪 ， 但是在数学中 ， 有时候就是要运用直觉做出尝试 ， 然后看看逻辑把我们带向何方 。
我们讲对数函数写成极限的形式 ， 然后代入我们对Gamma函数的定义式中 。 首先 ， 回忆一下：

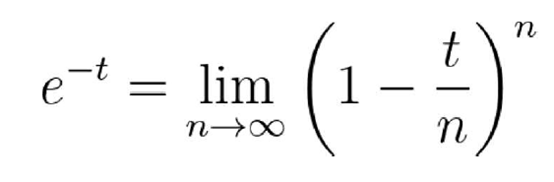
文章图片

这可以用多种方法证明 。 一个很显然的路子就是用洛必达法则求极限 。 但在这里 ， 我们用另一种方法 。 记得闭形式几何级数吗：

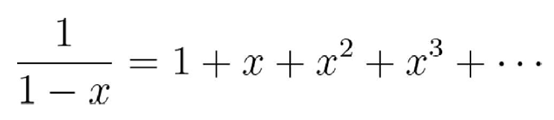
文章图片

这在|x|<1的情况下成立 。
注意 ， 若把x替换成-x ， 就得到：

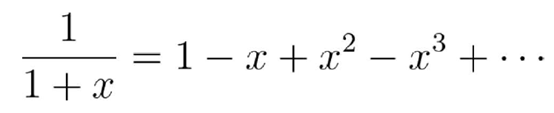
文章图片

现在我们可以对两侧进行进一步操作：

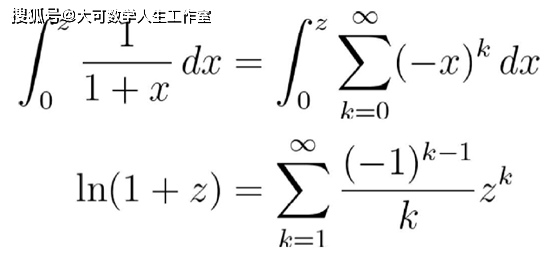
文章图片

假设n>x ， 然后可以做代换z=x/n:

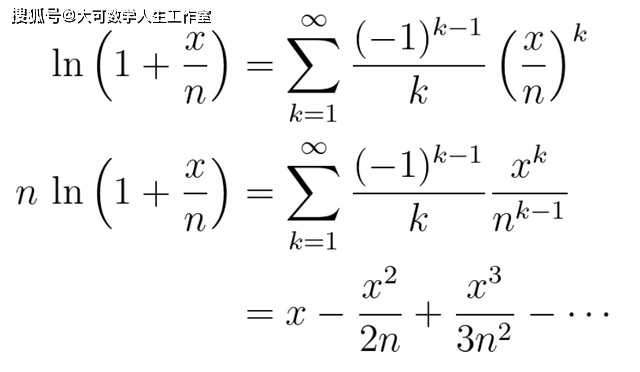
文章图片

现在 ， 如果我们取n趋向于无穷的极限 ， 显然有：

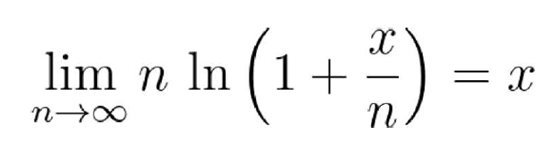
文章图片

以这个结果作为工具 ， 算出最终的结果就是一件十分直接的事情了：