下面的例子展示了这种运算的工作方式 。 它将输入平展为 16×1 的矩阵 ， 并将卷积核转换为一个稀疏矩阵（4×16） 。 然后 ， 在稀疏矩阵和平展的输入之间使用矩阵乘法 。 之后 ， 再将所得到的矩阵（4×1）转换为 2×2 的输出 。

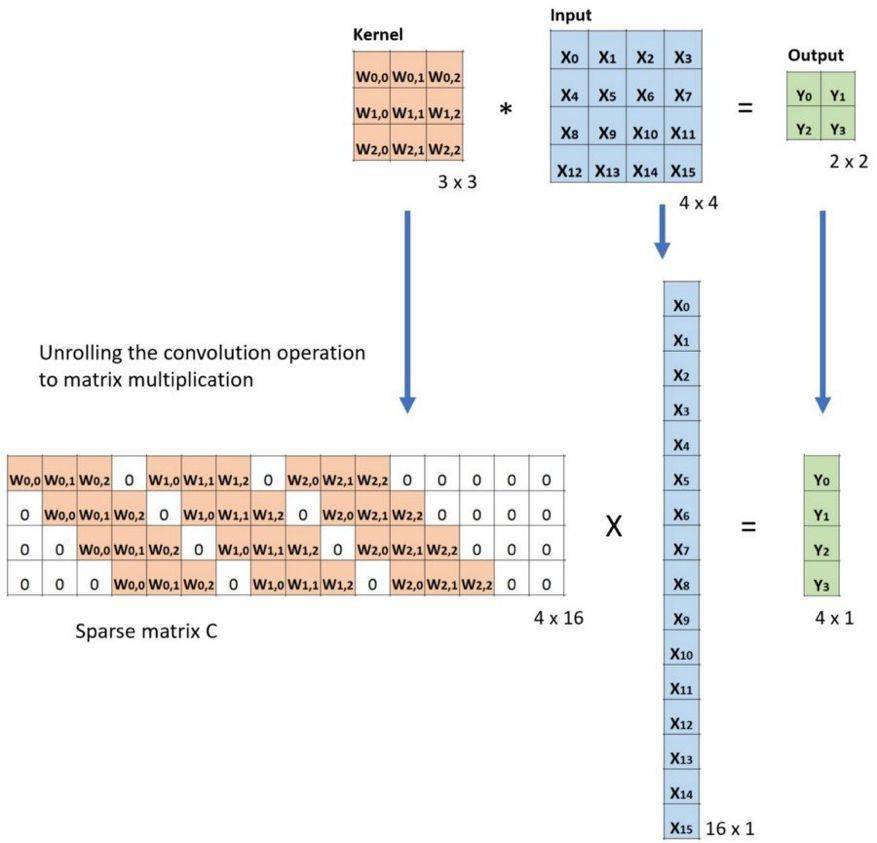
文章图片

卷积的矩阵乘法：将 Large 输入图像（4×4）转换为 Small 输出图像（2×2）
现在 ， 如果我们在等式的两边都乘上矩阵的转置 CT ， 并借助「一个矩阵与其转置矩阵的乘法得到一个单位矩阵」这一性质 ， 那么我们就能得到公式 CT x Small = Large ， 如下图所示 。

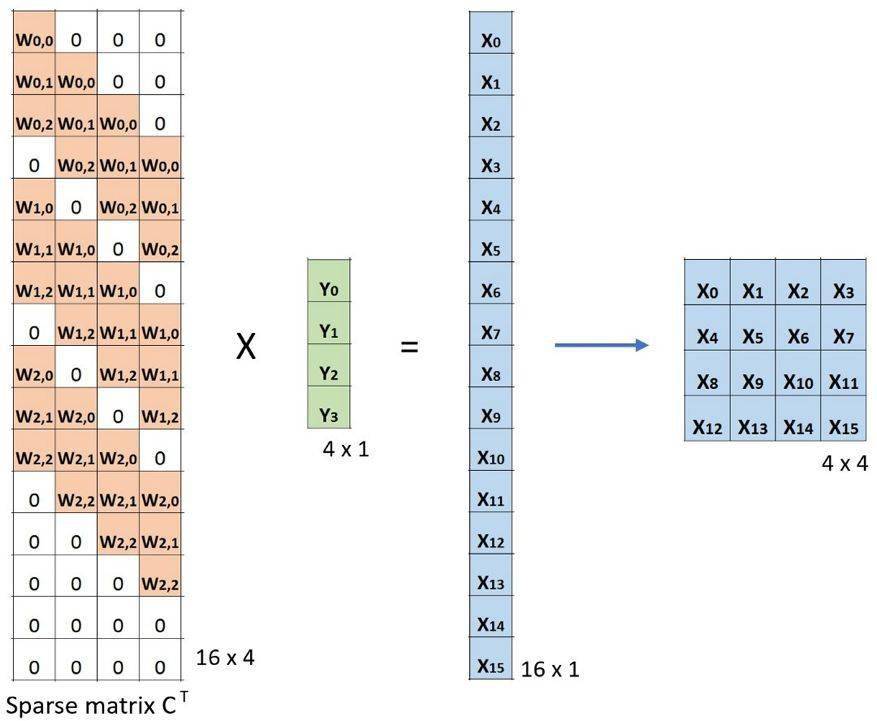
文章图片

卷积的矩阵乘法：将 Small 输入图像（2×2）转换为 Large 输出图像（4×4）
这里可以看到 ， 我们执行了从小图像到大图像的上采样 。 这正是我们想要实现的目标 。 现在 。 你就知道「转置卷积」这个名字的由来了 。
转置矩阵的算术解释可参阅：https://arxiv.org/abs/1603.07285
扩张卷积（Atrous 卷积）
扩张卷积由这两篇引入：

• https://arxiv.org/abs/1412.7062 ；
• https://arxiv.org/abs/1511.07122

这是一个标准的离散卷积：

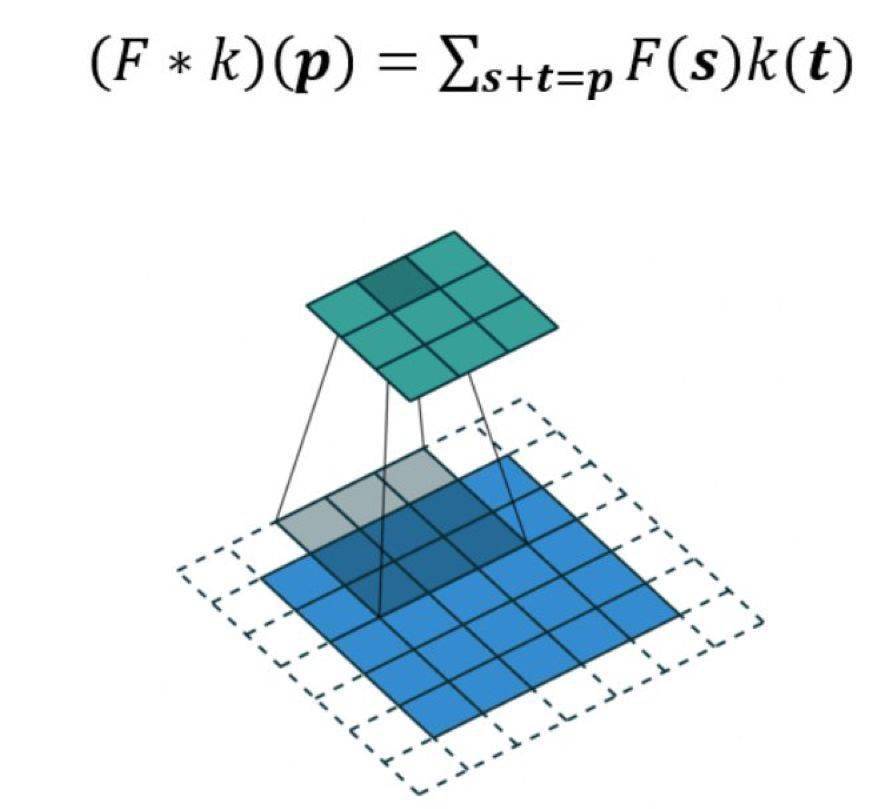
文章图片

扩张卷积如下：
当 l=1 时 ， 扩张卷积会变得和标准卷积一样 。

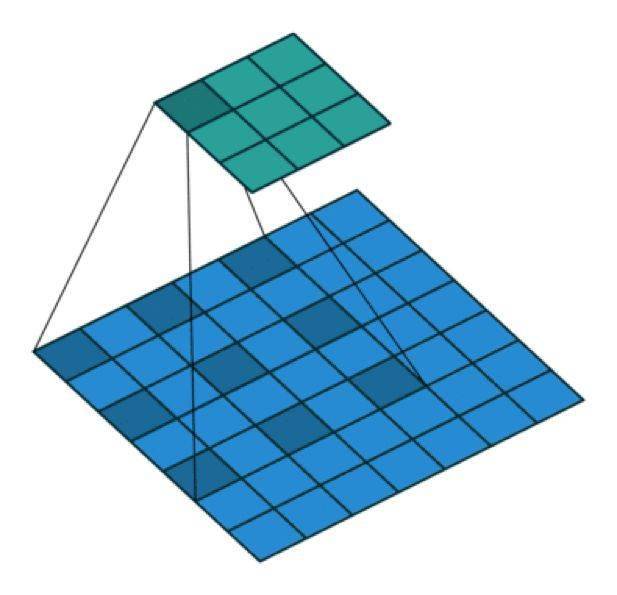
文章图片

扩张卷积
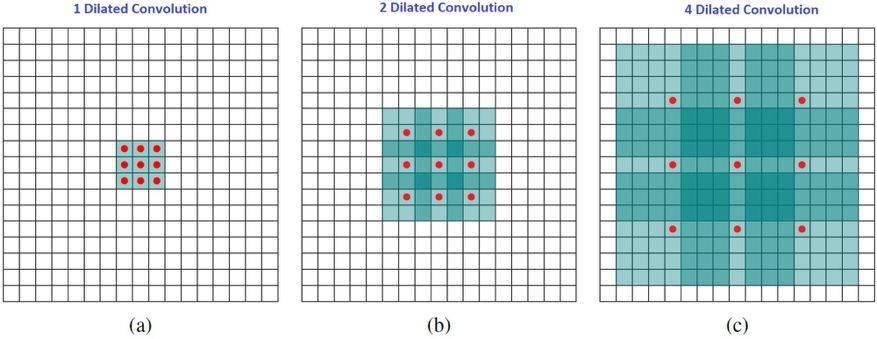
直观而言 ， 扩张卷积就是通过在核元素之间插入空格来使核「膨胀」 。 新增的参数 l（扩张率）表示我们希望将核加宽的程度 。 具体实现可能各不相同 ， 但通常是在核元素之间插入 l-1 个空格 。 下面展示了 l = 1, 2, 4 时的核大小 。

文章图片

扩张卷积的感受野 。 我们基本上无需添加额外的成本就能有较大的感受野 。
在这张图像中 ， 3×3 的红点表示经过卷积后 ， 输出图像是 3×3 像素 。 尽管所有这三个扩张卷积的输出都是同一尺寸 ， 但模型观察到的感受野有很大的不同 。 l=1 时感受野为 3×3 ， l=2 时为 7×7 。 l=3 时 ， 感受野的大小就增加到了 15×15 。 有趣的是 ， 与这些操作相关的参数的数量是相等的 。 我们「观察」更大的感受野不会有额外的成本 。 因此 ， 扩张卷积可用于廉价地增大输出单元的感受野 ， 而不会增大其核大小 ， 这在多个扩张卷积彼此堆叠时尤其有效 。
论文《Multi-scale context aggregation by dilated convolutions》的作者用多个扩张卷积层构建了一个网络 ， 其中扩张率 l 每层都按指数增大 。 由此 ， 有效的感受野大小随层而指数增长 ， 而参数的数量仅线性增长 。
这篇论文中扩张卷积的作用是系统性地聚合多个比例的形境信息 ， 而不丢失分辨率 。 这篇论文表明其提出的模块能够提升那时候（2016 年）的当前最佳形义分割系统的准确度 。 请参阅那篇论文了解更多信息 。
可分卷积
某些神经网络架构使用了可分卷积 ， 比如 MobileNets 。 可分卷积有空间可分卷积和深度可分卷积 。
1、空间可分卷积
空间可分卷积操作的是图像的 2D 空间维度 ， 即高和宽 。 从概念上看 ， 空间可分卷积是将一个卷积分解为两个单独的运算 。 对于下面的示例 ， 3×3 的 Sobel 核被分成了一个 3×1 核和一个 1×3 核 。