文章图片

和

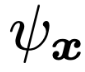
文章图片

分别是针对几何和非几何消息的聚合函数 。 除此以外 ，针对非几何信息的消息函数

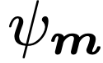
文章图片

是对于输入

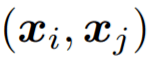
文章图片

来说 G - 不变的 。 而针对几何信息的

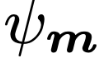
文章图片

消息函数则是对于输入

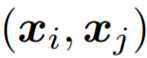
文章图片

来说 G - 等变的 。
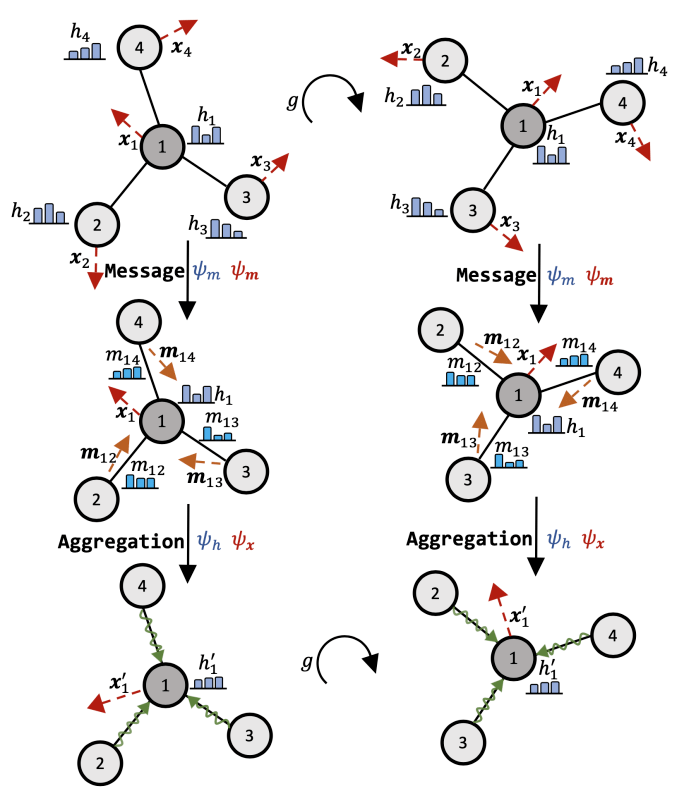
下图展示了这一通用框架的操作：

文章图片

基于以上的通用框架 ， 我们在下表总结了当前主流的等变图神经网络模型 。 与此同时 ， 基于消息表示的类别不同 ， 我们将现有的等变图神经网络模型分为三大类：不可约表示(Irreducible Representation) ， 正则表示(Regular Representation) 和标量化(Scalarization ).
基于不可约表示信息的模型
这类模型基于表示论中关于紧群的线性表示可以拆解为一系列的不可约表示的直积这一理论 。 从而在 SE(3) 群中构建满足等变性质的消息模型 。 例如 ， 在 TFN 中：

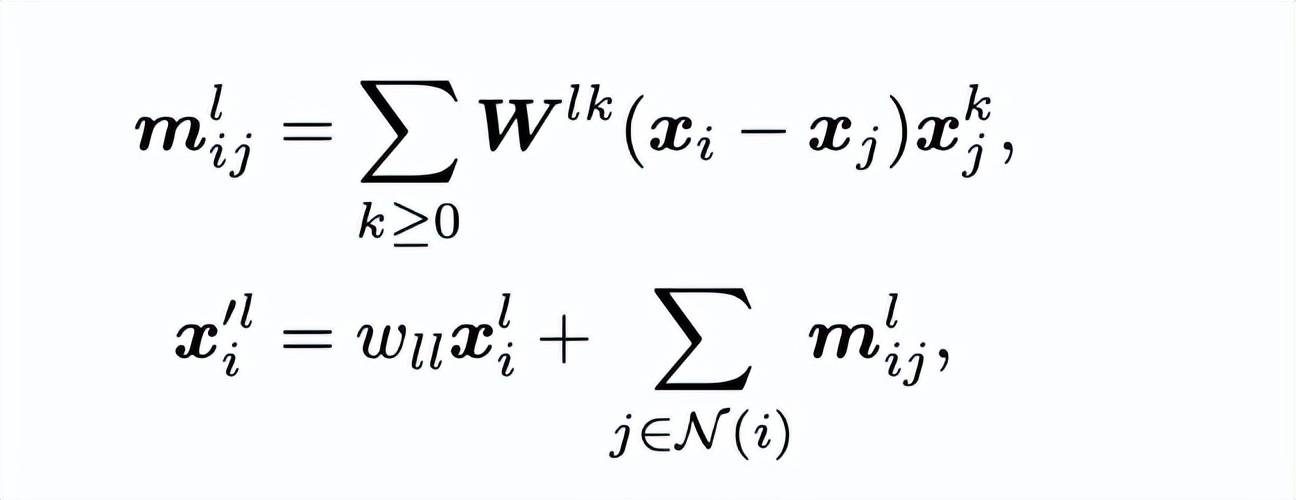
文章图片

TFN 层利用 Clebsch-Gordan 系数的性质构造了一个对于任意旋转参数

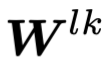
文章图片

， 对于任意属于 SO(3)的旋转操作都等变 。
有大量的工作基于 TFN 结构做了相应的扩展 ， 例如加入 Attention 机制 ，引入非线性的 Clebsch-Gordan 系数等 。 但是这类方法计算复杂度都较高 ， 且不可约表示仅仅适用于特定的群 。 这约束了这类模型的表达能力 。
基于正则表示信息的模型
另一类的工作尝试利用群的正则表示来构造群卷积操作 。 这里的代表性工作李卷积（LieConv）通过 Lifting 操作将输入映射到群中的元素 ， 然后利用 PointConv 完成群卷积的离散化计算 。 在我们的符号约定下 ， 李卷积可以表示为：

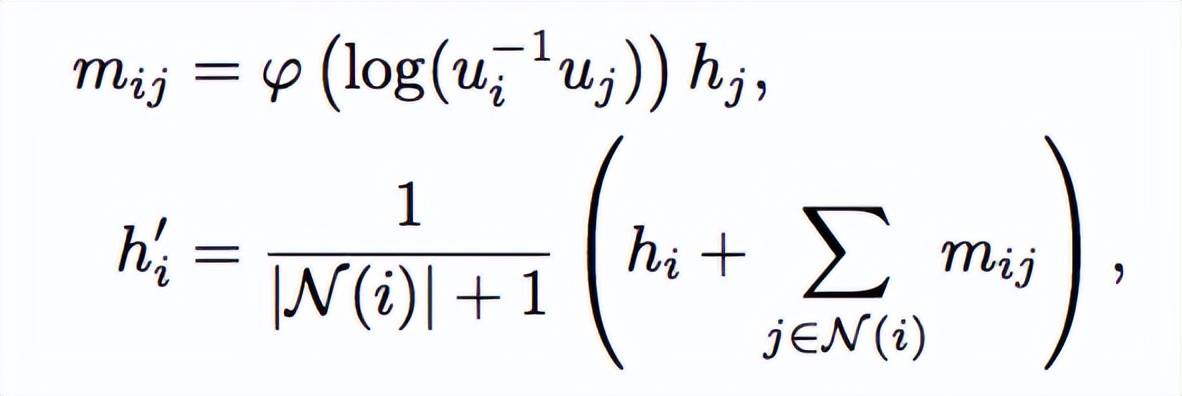
文章图片

其中

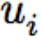
文章图片

是

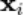
文章图片

在群中的映射元素 ， log 将群元映射到对应的李代数 ，

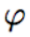
文章图片

是一个 MLP 。 通过这种构造 ， 李卷积中对于h_i的更新实现了对于任意李群以及其离散子群的不变性 。 LieTransformer 基于此思想 ， 引入了自注意力机制来进一步提高模型的性能 。 基于李群正则表示的模型在群的选取上更加灵活 ， 但是由于要进行离散化和采样 ， 需要在效率和性能之间做出权衡 。 同时 ， 以上的更新只考虑了标量信息 h ， 但难以直接推广到对几何信息 x 的更新 ， 除非综合哈密顿网络等工作中的更新方法 。
标量化
去基于群表示论的途径外 ， 很多工作采用了一种基于标量化的建模等变性质的方法 。 这类标量化的方法先将几何特征转化为一些不变的标量 ， 然后利用 MLP 等网络结构来得到一个标量变化 ， 最后将这个变化加回到原有的几何特征上从而得到等变性 。 这种标量化的方法最早是由 SchNet 和 DimNet 提出 ， 不过仅仅考虑了模型不变的部分 。 SphereNet 在之前工作的基础上进一步考虑了在消息传播网络上扭转角的变化 。 EGNN 作为在标量化里面一个重要的工作 ， 提出了一个非常灵活的框架：