函数连续和可导的关系,函数连续与可导之间的关系 _函数

函数连续与可导之间的关系关于函数的可导导数和连续的关系：
1、连续的函数不一定可导。
2、可导的函数是连续的函数。
3、越是高阶可导函数曲线越是光滑。
4、存在处处连续但处处不可导的函数。

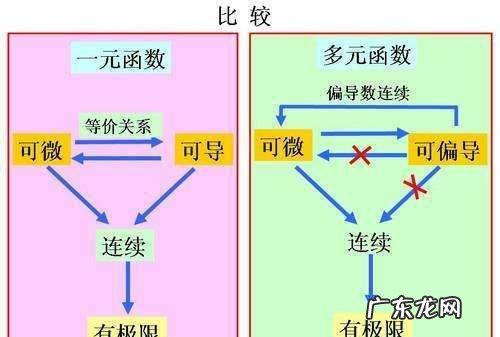
文章插图
在数学中，一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定（相对于全导数，在其中所有变量都允许变化）。偏导数在向量分析和微分几何中是很有用的。
偏导数的求法：
【函数连续和可导的关系,函数连续与可导之间的关系】当函数 z=f(x,y) 在 (x0,y0)的两个偏导数 f'x(x0,y0) 与 f'y(x0,y0)都存在时，我们称 f(x,y) 在 (x0,y0)处可导。如果函数 f(x,y) 在域 D 的每一点均可导，那么称函数 f(x,y) 在域 D 可导。
此时，对应于域 D 的每一点 (x,y) ，必有一个对 x (对 y )的偏导数，因而在域 D 确定了一个新的二元函数，称为 f(x,y) 对 x (对 y )的偏导函数。
一元函数可导与连续的关系在某点可导,则在这点必然连续.但连续不一定可导,假如这点是两条曲线的交点就不一定可导.同样,如果在某个区间可导,那么在这个区间必然连续.
用例子说说单调性问题.例如对于三次函数图像,通常都两个极值点,一个极大点,一个极小点,在这两个极值点之间曲线是连续的,导函数的符号会从大于零转换到小于零(或从小于零转换到大于零),恰恰在这符号变化点处(拐点),导函数不存在,这就是要求在该区间必须是单调的.
请观察下面图像中的Q点.

文章插图
函数连续性和可导性之间有什么关联吗函数连续性和可导性的关系如下：
连续的函数不一定可导；可导的函数是连续的函数；越是高阶可导函数曲线越是光滑；存在处处连续但处处不可导的函数。
拓展资料
函数的连续性和可导性是微积分中两个重要的概念。连续性是指函数在定义域内不存在跳跃或断裂的情况，而可导性则是指函数在某一点处存在切线斜率的概念。
一个函数在某一点处连续，意味着当自变量趋近于该点时，函数值也趋近于该点对应的函数值。换句话说，函数值的变化是平稳、连续的。形式化地，对于函数f(x) ，如果对于定义域内的任意x=a，当x趋近于a时，f(x)也趋近于f(a)，那么可以说函数f(x)点a处连续。

文章插图
一个函数在某一点处可导，意味着该点存在唯一的切线，并且切线的斜率存在。可导性与连续性有着密切的关系。具体来说，如果函数f(x)在某一点a处可导，那么函数f(x)在点a处必然连续。这是因为可导性要求函数在某一点的极限存在，并且极限值等于该点处的函数值，而连续性要求函数在该点的极限等于该点处的函数值。因此，可导性是连续性的一个更强的条件。
连续性不一定能够保证可导性。有些函数在某一点处连续，但在该点处没有切线斜率，因此不可导。例如，在函数f(x)=|x|中，当x=0时，虽然该函数在点x=0处连续，但由于左右导数不相等，不存在唯一的切线斜率，因此该函数在点x=0处不可导。
值得注意的是，当函数在某一点处可导时，它必然在该点处连续，但连续性并不保证可导性。这就意味着，函数的连续性是可导性的一个充分条件，但不是必要条件。

文章插图
关于连续与可导的性质
1、连续性和可导性使得函数在数学建模和实际问题中具有重要的应用价值。连续性能够研究函数在定义域内的各种性质，如函数的极值、函数图像的形态等。可导性则提供了研究函数局部性质的工具，如切线斜率、导数的变化等。这些概念在物理学、经济学、工程学等学科中都得到广泛的应用。
2、连续函数的基本运算法则和可导函数的求导法则为求解函数的极限、最值、方程等问题提供了便利。通过对连续函数的性质和可导函数的导数进行分析，可以探索函数的特殊性质，并进一步解决实际问题。
3、连续性和可导性还与数学分析中的一些重要定理和概念相关。例如，连续函数的最值定理和介值定理等，以及可导函数的中值定理和泰勒展开等。这些定理和概念为研究函数的性质和求解各类问题提供了强有力的工具和方法。
偏导连续与可微的关系是什么连续与可导的关系：
1、连续的函数不一定可导；
2、可导的函数是连续的函数；
3、越是高阶可导函数曲线越是光滑；
4、存在处处连续但处处不可导的函数。

文章插图
可导：
微积分是在17世纪末由英国物理学家、数学家牛顿和德国数学家莱布尼茨建立起来的。微积分是由微分学和积分学两部分组成，微分学是基础。微分学的基本概念是导数和微分，核心概念是导数。导数反应了函数相对于自变量的变化率问题。

特别声明：本站内容均来自网友提供或互联网，仅供参考，请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系，我们将在24小时内删除。