机器之心报道
编辑:陈萍、杜伟
非凸优化问题被认为是非常难求解的 , 因为可行域集合可能存在无数个局部最优点 , 通常求解全局最优的算法复杂度是指数级的(NP 困难) 。 那么随机梯度下降能否收敛于非凸函数?针对这一问题 , 众多网友进行了一番讨论 。在机器学习领域 , 我们经常会听到凸函数和非凸函数 , 简单来讲 , 凸函数指的是顺着梯度方向走 , 函数能得到最优解, 大部分传统机器学习问题都是凸的 。 而非凸指的是顺着梯度方向走能够保证是局部最优 , 但不能保证是全局最优 , 深度学习以及小部分传统机器学习问题都是非凸的 。
在寻求最优解的过程中 , 研究者通常采用梯度下降算法 。 近日 , reddit 上的一个热议帖子 , 帖子内容为「随机梯度下降能否收敛于非凸函数?」
【非凸函数上,随机梯度下降能否收敛?能有条件,比凸函数收敛更难】

文章图片
原贴内容包括:大量的研究和工作表明梯度下降算法可以收敛于(确定性)凸函数、可微和利普希茨连续函数:

文章图片
然而 , 在非凸函数领域 , 基于梯度下降算法(例如随机梯度下降)的收敛程度有多大 , 目前看来研究还不够充分 。 例如 , 神经网络中的损失函数几乎是非凸的 。 非凸函数通常有鞍点(即损失函数的一阶导数为 0 的点) , 我们可以将这些鞍点视为「陷阱」 , 鞍点的存在阻止梯度下降到最优点 , 因为梯度下降在导数为 0 时不能向前移动 。
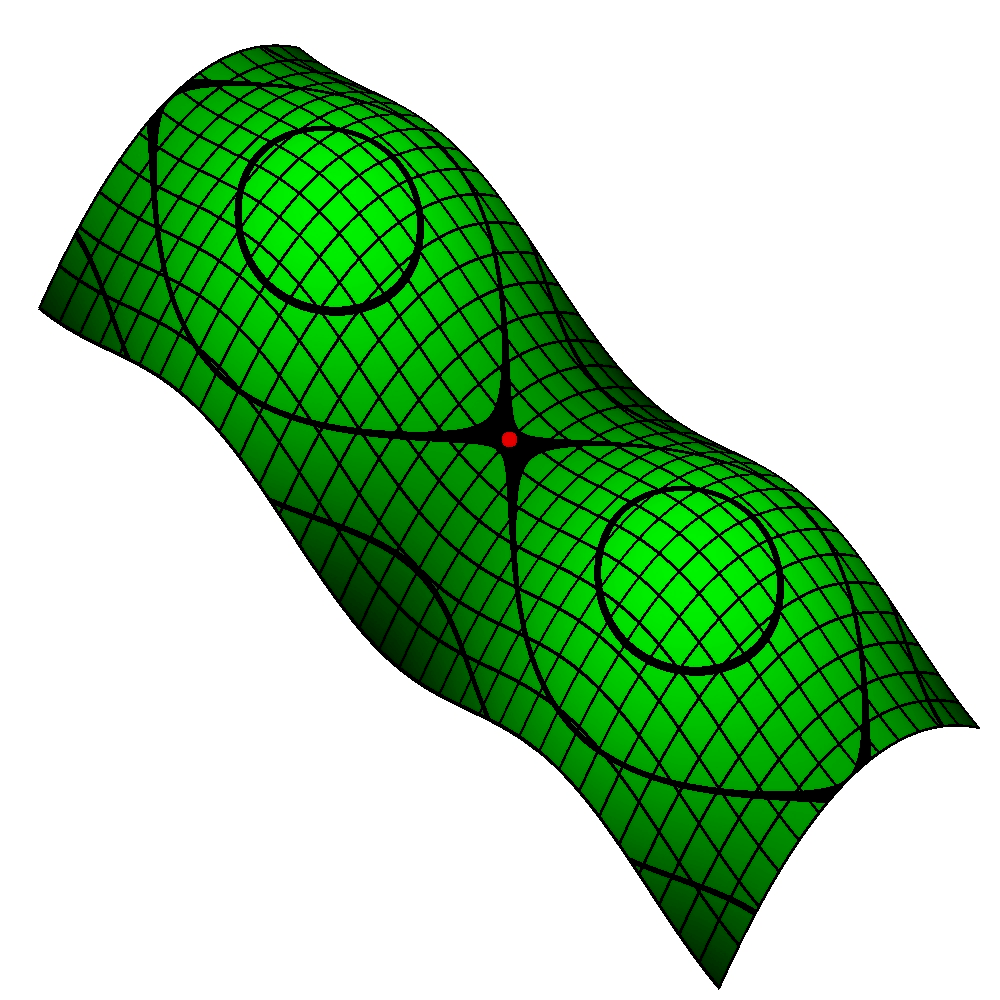
文章图片
两座山中间的鞍点(双纽线的交叉点)
在机器学习、深度学习中使用的优化算法除了常见的梯度下降和随机梯度下降 , 还包括其他版本 , 例如 Nesterov 动量、Adam、RMSprop 等几种优化器 , 这些优化器旨在让梯度远离鞍点 。 对于这些算法 , 发帖者很熟悉 , 但 ta 比较感兴趣的是随机梯度下降算法本身的理论局限性有哪些?
在过去的几周里 , 发帖人一直在阅读有关这个主题的文章 , 但是理解其中一些结果所需的数学知识远远超出了 ta 的能力范围 。 为了弄清这个问题 , ta 也查阅了大量的文献 , 以下是其中 2 篇:
文献 1:Stochastic Gradient Descent for Nonconvex Learning without Bounded Gradient Assumptions
- 随机梯度下降被大量应用于非凸函数 , 但研究者对非凸函数的随机梯度下降的理论尚未完全了解(目前仅对凸函数的随机梯度下降有了解);
- 现阶段随机梯度下降要求对梯度的一致有界性施加一个假设;
- 论文作者建立了非凸函数随机梯度下降理论基础 , 使有界假设可以消除而不影响收敛速度;
- 论文建立了应用于非凸函数随机梯度下降收敛的充分条件和最优收敛速度 。
- 尽管随机梯度下降的最新进展值得注意 , 但这些进展是建立在对正在优化的函数施加了某些限制(例如 , 凸性、全局利普希茨连续等)的基础之上;
- 作者证明 , 对于一般类的非凸函数 , 随机梯度下降迭代要么发散到无穷大 , 要么收敛到概率为 1 的静止点;
特别声明:本站内容均来自网友提供或互联网,仅供参考,请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系,我们将在24小时内删除。
