舍弃谱归一化，这篇ICCV’21论文用梯度归一化训练GAN，效果极好( 二 ) _信息快讯

论文地址：https://arxiv.org/pdf/2109.02235.pdf
代码地址：https://github.com/basiclab/GNGAN-PyTorch
研究者指出，与 SN 不同， GN 的利普希茨常量不会以神经网络的乘法形式衰减，这是因为我们将判别器视为一种通用的函数近似器，计算出的归一化项与中间层无关。梯度归一化方法有以下两个良好的特性：（1）归一化同时满足模型级、非基于采样、硬约束三个特性，并且不会引入额外的超参数。（2）GN 的实现十分简单，可以兼容各种网络架构。
预备知识
生成对抗网络
生成器 G:R^d_zR^n 和判别器 D:R^nR 之间的博弈可以被形式化定义为如下的极大极小目标：

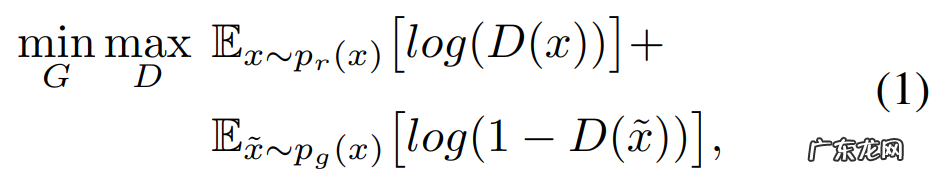
文章插图

其中， p_r(x) 是真实数据分布， p_g=G_*(p_z) 。 * 是前推测度， p_z 是 d_z 维的先验分布。当判别器 D 最优时，可以保证生成器 G 收敛到真实分布 p_r(x) 上。然而，训练 GAN 会遇到许多问题，除了梯度消失和梯度爆炸之外，还有两种原因造成不稳定的训练：首先，优化上面的目标函数（1）等价于最小化 p_g(x) 和 p_r(x) 之间的 JS 散度。如果 p_g(x) 和 p_r(x) 并未重合，则 JS 散度会为一个常数，并导致梯度消失；第二，有限的真实样本往往会造成判别器的过拟合，间接造成围绕真实样本的梯度爆炸。
Wasserstein GAN (WGAN)
研究人员提出了 WGAN，通过最小化 p_g(x) 和 p_r(x) 之间的 Wasserstein-1 距离来优化 GAN 。

文章插图

其中， L_D 是判别器 D 的利普希茨常数。 L_D 定义如下：

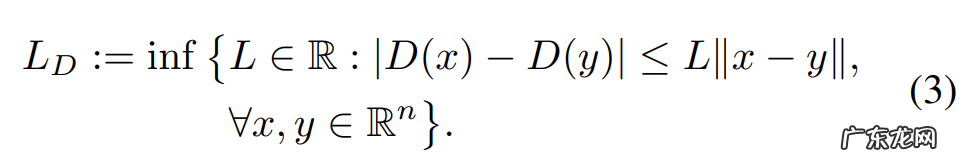
文章插图

换而言之， L_D 是使得下式成立的最小实数：

文章插图

值得注意的是，度量 ||·|| 可以是任意的向量范数。 WGAN 的判别器旨在通过在满足利普希茨约束 (4) 的条件下最大化目标函数 (2) 来近似 Wasserstein 距离。实际上，我们可以通过将函数与放缩因子相乘来缩放利普希茨常数，因此对利普希茨常数 L_D 的不同选择不会对结果产生影响。此外，学界已经证明， Wasserstein 距离在学习的分布由低维流形支撑时比 KL 距离更加敏感。显然，近似的误差率与判别器的容量有关。如果判别器可以在一个较大的函数空间内搜索，它就可以更加精确地近似 Wasserstein 距离，从而使生成器更好地建模真实分布。同时，利普希茨约束限制了值表面的倾斜度，缓解了判别器的过拟合问题。
符号定义
定义 1：令 f_K:R^nR 为 K 层网络，它可以被形式化定义为一个由一组仿射变换组成的函数：

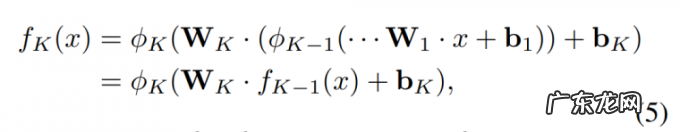
文章插图

其中， W_K∈R^d_K×d_K-1 以及 b_K∈R^d_K 是第 K 层的参数， d_K 是第 K 层的目标维度， φ_K 是第 K 层的元素级的非线性激活函数。 f_K, k ∈ 代表前 K 层组成的子网络。
为了分析带有层级别约束的网络性能，我们将层级别的利普希茨网络定义如下。
定义 2：令 f_K : R^n R 为第 K 层网络，如果 L_k ≤ L, k ∈ ，则 f_K 是层级别的 L – 利普希茨约束，其中 L_K 为第 k 层的利普希茨常数。
引理 3：令 f : R^n R 为连续的可微函数，且 L_f 为 f 的利普希茨常数。则利普希茨约束 (4) 等价于

文章插图

假设 4：令 f : R^n R 为神经网络建模的连续函数，网络 f 的所有激活函数是分段线性函数。则函数 f 几乎肯定是可微的。

特别声明：本站内容均来自网友提供或互联网，仅供参考，请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系，我们将在24小时内删除。

舍弃谱归一化，这篇ICCV&#8217;21论文用梯度归一化训练GAN，效果极好( 二 )

舍弃谱归一化，这篇ICCV’21论文用梯度归一化训练GAN，效果极好( 二 )