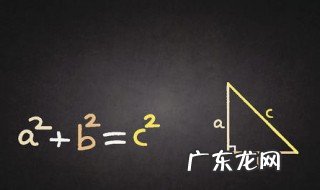
文章插图
1、在平面上的一个直角三角形中 , 两个直角边边长的平方加起来等于斜边长的平方 。
2、勾股定理是一个基本的几何定理 , 指直角三角形的两条直角边的平方和等于斜边的平方 。中国古代称直角三角形为勾股形 , 并且直角边中较小者为勾 , 另一长直角边为股 , 斜边为弦 , 所以称这个定理为勾股定理 , 也有人称商高定理 。
【勾股定理 勾股定理是几年级学的】3、勾股定理现约有500种证明方法 , 是数学定理中证明方法最多的定理之一 。勾股定理是人类早期发现并证明的重要数学定理之一 , 用代数思想解决几何问题的最重要的工具之一 , 也是数形结合的纽带之一 。在中国 , 周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例 。在西方 , 最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派 , 他用演绎法证明了直角三角形斜边平方等于两直角边平方之和 。
- flag是什么梗
- 尼古拉斯赵四是什么梗
- 沈家门是什么区 沈家门属于哪个省哪个市
- 野生鲫鱼的辨别 怎么分辨鲫鱼是野生的
- 百年福牌黄金:是黄金还是骗局?
- 疟疾的症状是什么
- 缺钙怕冷吗
- 平邮到付件是什么意思 什么是平邮件和到付件
- 油镜用的是什么油 什么叫油镜
- 雪藏是什么意思:艺人被雪藏是什么意思 雪藏艺人什么意思
特别声明:本站内容均来自网友提供或互联网,仅供参考,请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系,我们将在24小时内删除。
