函数连续的充要条件,函数连续的充要条件 _函数

函数连续的充要条件函数连续的充要条件是：如果函数f在点a连续，那么f在点a的左极限、右极限和函数值都存在且相等
1、如果函数f在点a连续，那么f在点a的左极限、右极限和函数值都存在且相等即lim_（x->a-）f（x）=f（a）=lim_（x->a+）f（x）。这就是所谓的“三合一”原则。
2、函数的连续性是数学分析中的一个重要概念，它描述了函数在某一点或某一区间内的性质。一个函数在某个点连续，意味着函数在该点的极限存在且等于函数值；如果函数在区间内的每一点都连续，那么这个函数就是在整个区间上连续的。

文章插图
3、如果函数f在区间（a，b）上连续，那么f在区间端点的值相等，即f（a）=f（b）。同时，如果函数f在区间（a，b）上连续，且在开区间（a，b）内可导，那么f在区间（a，b）上必定可积。
函数的相关信息
1、函数是数学中的一种基本概念，它描述了两个量之间的依赖关系。在函数中，一个量被称为自变量，另一个量被称为因变量或函数值。函数通常用符号f来表示，自变量的取值范围称为定义域，函数值的取值范围称为值域。
2、函数可以是一元函数，即只涉及一个自变量和一个因变量；也可以是多元函数，即涉及多个自变量和多个因变量。函数还可以是离散的或连续的。离散函数在其定义域内的任意两点之间都有定义，而连续函数在其定义域内的每一点都有定义。

文章插图
3、函数的概念在数学、物理、工程等许多领域都有广泛的应用，例如，物理学中的力和加速度之间的关系可以用函数来描述；经济学中的供求关系也可以用函数来表示。此外，函数还是计算机科学中的重要概念，许多编程语言都提供了对函数的支持。
函数连续性的三个条件是什么连续的充要条件是：
1、左右导数存在且相等是可导的充分必要条件。
2、可导必定连续。
3、连续不一定可导。所以，左右导数存在且相等就能保证该点是连续的。仅有左右导数存在且该点连续不能保证可导：例如y=|x|在x=0点。
因变量关于自变量是连续变化的，连续函数在直角坐标系中的图像是一条没有断裂的连续曲线。由极限的性质可知，一个函数在某点连续的充要条件是它在该点左右都连续。

文章插图
连续函数是指函数y=f（x）当自变量x的变化很小时，所引起的因变量y的变化也很小。例如，气温随时间变化，只要时间变化很小，气温的变化也是很小的；又如，自由落体的位移随时间变化，只要时间变化足够短，位移的变化也是很小的。
对于这种现象，因变量关于自变量是连续变化的，连续函数在直角坐标系中的图像是一条没有断裂的连续曲线。由极限的性质可知，一个函数在某点连续的充要条件是它在该点左右都连续。
函数连续的充要条件是什么解：
x→0＋
lim｜sinx｜＝limsinx＝0＝sin0
x→0－
limsinx＝lim－sinx＝0＝sin0
左右都连续．所以连续
x→0＋
lim（｜sinx｜－｜sin0）｜／（x－0）＝limsinx／x＝1
x→0－
lim（｜sinx｜－｜sin0）｜／（x－0）＝lim－sinx／x＝－1
左右导数不等，所以不可导。
连续性：y在X的领域内处有定义，而且y在X趋向于0时极限存在，而且极限值等于y在X＝0的值。证明极限存在，要看左右极限是否存在且相等，像这函数，左右极限都存在，且都等于0，而且极限值等于函数值。
可导性：先对函数进行求导，再求其在X＝0处左右极限是否存在且相等，如果不存在，则不可导，如果存在可是不相等，也不可导。

文章插图
扩展资料
函数的连续性：
在定义函数的连续性之前先了解一个概念——增量设变量x从它的一个初值x1变到终值x2，终值与初值的差x2－x1就叫做变量x的增量，记为：△x即：△x＝x2－x1增量△x可正可负。
设函数在区间［a ， b）内有定义，如果右极限存在且等于，即：＝，那么就称函数在点a右连续。一个函数在开区间（a，b）内每点连续。
则为在（a，b）连续，若又在a点右连续， b点左连续，则在闭区间［a ， b］连续，如果在整个定义域内连续，则称为连续函数。
注：一个函数若在定义域内某一点左、右都连续，则称函数在此点连续，否则在此点不连续。注：连续函数图形是一条连续而不间断的曲线。
函数连续的充分必要条件是什么?函数f(x)在x0连续,当且仅当f(x)满足以下三个条件:
①f(x)在x0及其左右近旁有定义；
②f(x)在x0的极限存在；
③f(x)在x0的极限值与函数值f(x0)相等。
扩展资料：
间断点
如果函数

文章插图
在点

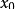
文章插图
处不连续，则称

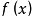
文章插图
在点

文章插图
处间断，并把

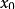
文章插图
称为

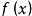
文章插图
的间断点。
【函数连续的充要条件,函数连续的充要条件】

特别声明：本站内容均来自网友提供或互联网，仅供参考，请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系，我们将在24小时内删除。