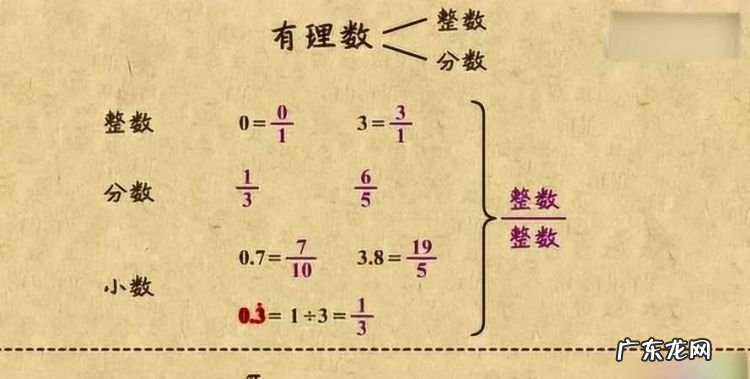
什么叫有理数,什么叫有理数 _什么

什么叫有理数有理数的定义：有理数是整数和分数的统称，是整数和分数的集合。无理数的定义：无理数是无限不循环小数，是所有非有理数的实数。无理数是指实数范围内不能表示成两个整数之比的数，比如圆周率。
有理数和无理数的区别
有理数和无理数都写成小数形式时,有理数能写成有限小数。所有的有理数都可以写成两个整数之比,而无理数却不能写成两个整数之比。常见的无理数有非完全平方数的平方根、π和e(其中后两者均为超越数)等。无理数的另一特征是无限的连分数表达式。无理数最早由毕达哥拉斯学派弟子希伯索斯发现。
有理数集是整数集的扩张。在有理数集，加法、减法、乘法、除法(除数不为零)4种运算通行无阻。无理数是指实数范围不能表示成两个整数之比的数。简单的说，无理数就是10进制下的无限不循环小数。

文章插图
什么是有理数有理数是整数和分数的统称,一切有理数都可以化成分数的形式.
详细：
有理数可分为整数和分数也可分为正有理数,0,负有理数.除了无限不循环小数以外的实数统称有理数.英文：rational number读音：yǒu lǐ shù整数和分数统称为有理数,任何一个有理数都可以写成分数m/n（m,n都是整数,且n≠0）的形式.任何一个有理数都可以在数轴上表示.其中包括整数和通常所说的分数,此分数亦可表示为有限小数或无限循环小数.这一定义在数的十进制和其他进位制（如二进制）下都适用.数学上,有理数是一个整数 a 和一个非零整数 b 的比(ratio),通常写作 a/b,故又称作分数.希腊文称为 λογο,原意为“成比例的数”(rational number),但中文翻译不恰当,逐渐变成“有道理的数”.无限不循环小数称之为无理数（例如：圆周率π）有理数和无理数统称为实数.所有有理数的集合表示为Q.

文章插图
什么是有理数有理数是整数和分数的统称，1切有理数都可以化成份数的情势。有理数可分为整数和分数也可分为3种，1；正有理数， 2；0，3；负有理数。除无穷不循环小数之外的实数统称有理数。英文：rationalnumber读音：yǒulǐshù整数和分数统称为有理数，任何1个有理数都可以写成份数m/n（m，n都是整数，且n≠0）的情势。任何1个有理数都可以在数轴上表示。其中包括整数和通常所说的分数，此分数亦可表示为有限小数或无穷循环小数。这1定义在数的10进制和其他进位制（如2进制）下都适用。数学上，有理数是1个整数a和1个非零整数b的比(ratio)，通常写作a/b ，故又称作分数。希腊文称为λογο，原意为“成比例的数”(rationalnumber) ，但中文翻译不恰当，逐步变成“有道理的数” 。无穷不循环小数称之为无理数（例如：圆周率π）有理数和无理数统称为实数。

文章插图
什么是有理数有理数的概念
1、有理数：整数和分数统称为有理数。
注意：
（1）有时为了研究的需要，整数也可以看作是分母为1的数，这时的分数包括整数。但是本节中的分数不包括分母是1的分数。
（2）因为分数与有限小数和无限循环小数可以互化，上述小数都可以用分数来表示，所以我们把有限小数和无限循环小数都看作分数。
（3）“0”即不是正数，也不是负数，但“0”是整数。
2、整数包括正整数、零、负整数。
3、分数包括正分数和负分数。
有理数的分类
1、按整数、分数的关系分类： 2、按正数、负数与0的关系分类：

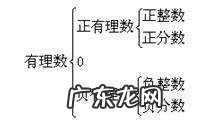
文章插图

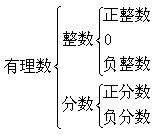
文章插图
有理数分类如上，无理数分类如下：
无理数
（1）无理数，也称为无限不循环小数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环。常见的无理数有非完全平方数的平方根、π和e（其中后两者均为超越数）等。无理数的另一特征是无限的连分数表达式。
（2）无理数是指实数范围内不能表示成两个整数之比的数。简单的说，无理数就是10进制下的无限不循环小数，如圆周率、√2等。也是开方开不尽的数。
（3）无理数和有理数共同组建了实数，实数，是有理数和无理数的总称。数学上，实数定义为与数轴上的点相对应的数。实数可以直观地看作有限小数与无限小数，实数和数轴上的点一一对应。
实数分类：
根据定义分类，也可以根据性质分类。
根据定义分类：

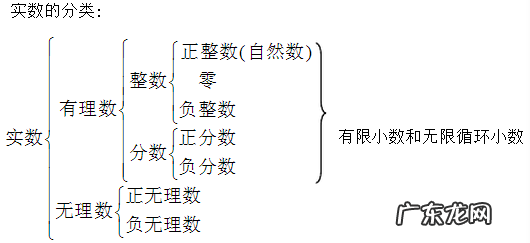
文章插图
根据性质分类：

文章插图
【什么叫有理数,什么叫有理数】

特别声明：本站内容均来自网友提供或互联网，仅供参考，请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系，我们将在24小时内删除。