原文链接：http://tecdat.cn/?p=21625
我们知道参数的置信区间的计算 ， 这些都服从一定的分布(t分布、正态分布） ， 因此在标准误前乘以相应的t分值或Z分值 。 但如果我们找不到合适的分布时 ， 就无法计算置信区间了吗？幸运的是 ， 有一种方法几乎可以用于计算各种参数的置信区间 ， 这就是Bootstrap 法 。
本文使用BOOTSTRAP来获得预测的置信区间 。 我们将在线性回归基础上讨论 。

1. > reg=lm(dist~speed,data=https://www.sohu.com/a/cars)
2. > points(x,predict(reg,newdata= https://www.sohu.com/a/data.frame(speed=x)))

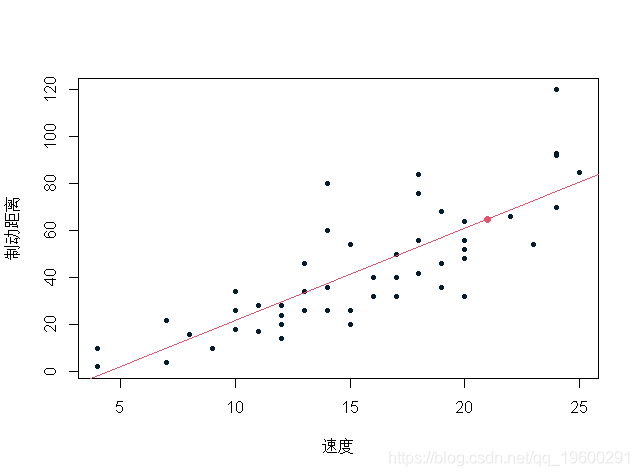
文章图片

这是一个单点预测 。 当我们想给预测一个置信区间时 ， 预测的置信区间取决于参数估计误差 。
预测置信区间 让我们从预测的置信区间开始

1. > for(s in 1:500){
2. + indice=sample(1:n,size=n,
3. + replace=TRUE)
4. + points(x,predict(reg,newdata=https://www.sohu.com/a/data.frame(speed=x)),pch=19,col="blue")

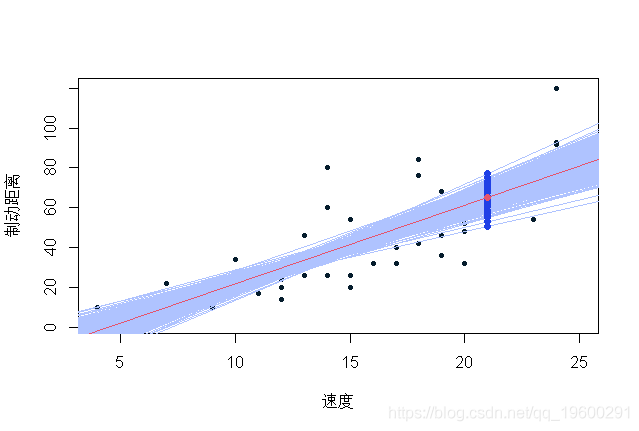
文章图片

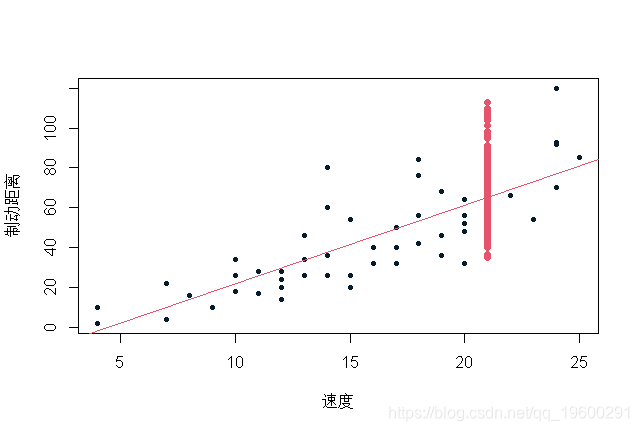
蓝色值是通过在我们的观测数据库中重新取样获得的可能预测值 。 值得注意的是 ， 在残差正态性假设下（回归线的斜率和常数估计值） ， 置信区间（90%）如下所示：
predict(reg,interval ="confidence",

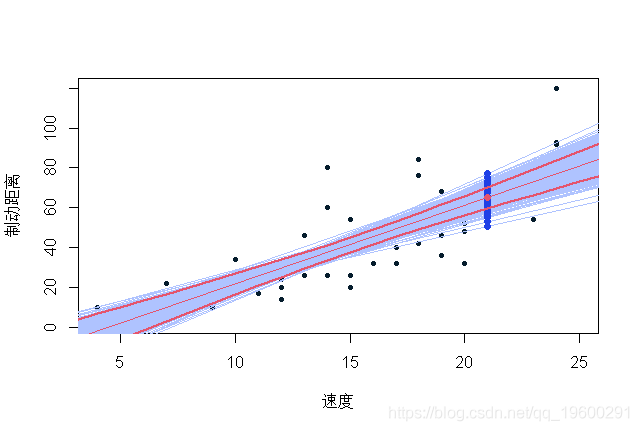
文章图片

【reg|拓端tecdat|R语言基于Bootstrap的线性回归预测置信区间估计方法】在这里 ， 我们可以比较500个生成数据集上的值分布 ， 并将经验分位数与正态假设下的分位数进行比较 ，

1. > hist(Yx,proba=TRUE
2. > boxplot(Yx,horizontal=TRUE
3. > polygon(c( x ,rev(x I]))))

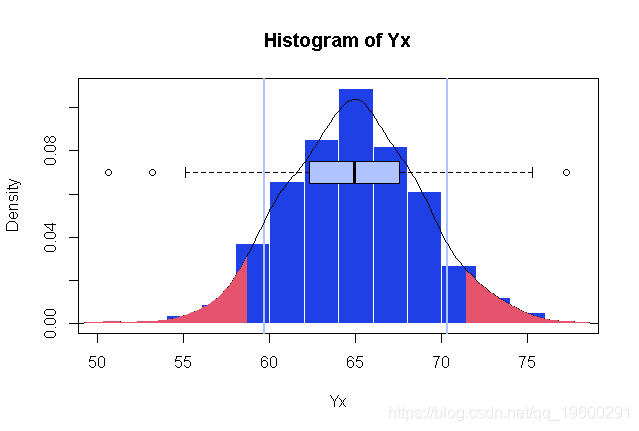
文章图片

可以看出 ， 经验分位数与正态假设下的分位数是可以比较的 。

1. > quantile(Yx,c(.05,.95))
2. 5% 95%
3. 58.63689 70.31281
4. + level=.9,newdata=https://www.sohu.com/a/data.frame(speed=x))
5. fit lwr upr
6. 1 65.00149 59.65934 70.34364

感兴趣变量的可能值 现在让我们看看另一种类型的置信区间 ， 关于感兴趣变量的可能值 。 这一次 ， 除了提取新样本和计算预测外 ， 我们还将在每次绘制时添加噪声 ， 以获得可能的值 。

1. > for(s in 1:500){
2. + indice=sample(1:n,size=n,
3. + base=cars[indice,]
4. + erreur=residuals(reg)
5. + predict(reg,newdata=https://www.sohu.com/a/data.frame(speed=x))+E

文章图片

在这里 ， 我们可以（首先以图形方式）比较通过重新取样获得的值和在正态假设下获得的值 ，

1. > hist(Yx,proba=TRUE)
2. > boxplot(Yx) abline(v=U[2:3)
3. > polygon(c(D$x[I,rev(D$x[I])

文章图片

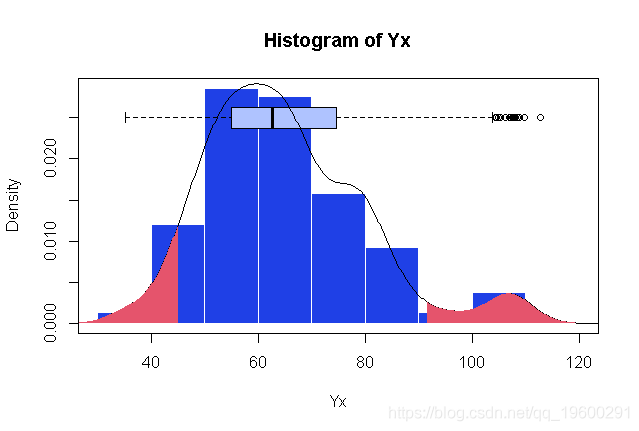
数值上给出了以下比较

1. > quantile(Yx,c(.05,.95))
2. 5% 95%
3. 44.43468 96.01357
4. U=predict(reg,interval ="prediction"
5. fit lwr upr
6. 1 67.63136 45.16967 90.09305

这一次 ， 右侧有轻微的不对称 。 显然 ， 我们不能假设高斯残差 ， 因为有更大的正值 ， 而不是负值 。 考虑到数据的性质 ， 这是有意义的（制动距离不能是负数） 。
然后开始讨论在供应中使用回归模型 。 为了获得具有独立性 ， 有人认为必须使用增量付款的数据 ， 而不是累计付款 。