原文链接：http://tecdat.cn/?p=21602
正则化(regularization)
正则化路径是在正则化参数lambda的值网格上计算套索LASSO或弹性网路惩罚的正则化路径 。 该算法速度快 ， 可以利用输入矩阵x中的稀疏性 ， 拟合线性、logistic和多项式、poisson和Cox回归模型 。 可以通过拟合模型进行各种预测 。 它还可以拟合多元线性回归 。 ”
例子
加载数据
这里加载了一个高斯(连续Y)的例子 。
as_data_frame(y)

1. ## # A tibble: 100 x 1
2. ## V1
3. ## <dbl>
4. ## 1 -1.2748860
5. ## 2 1.8434251
6. ## 3 0.4592363
7. ## 4 0.5640407
8. ## 5 1.8729633
9. ## 6 0.5275317
10. ## 7 2.4346589
11. ## 8 -0.8945961
12. ## 9 -0.2059384
13. ## 10 3.1101188
14. ## # ... with 90 more rows

初始岭回归
cv.glmnet执行k-折交叉验证 .

1. ## 执行岭回归
2. glmnet(x , y
3. ## “alpha=1”是套索惩罚, “alpha=0”是岭惩罚 。
4. alpha = 0)
5. ## 用10折CV进行岭回归
6. cv.glmnet(
7. ## 类型.测量：用于交叉验证的丢失 。
8. type.measure = "mse",
9. ## K = 10 是默认值 。
10. nfold = 10,
11. ##“alpha=1”是套索惩罚 ， “alpha=0”是岭惩罚 。
12. alpha = 0)
13. ## 惩罚vs CV MSE图

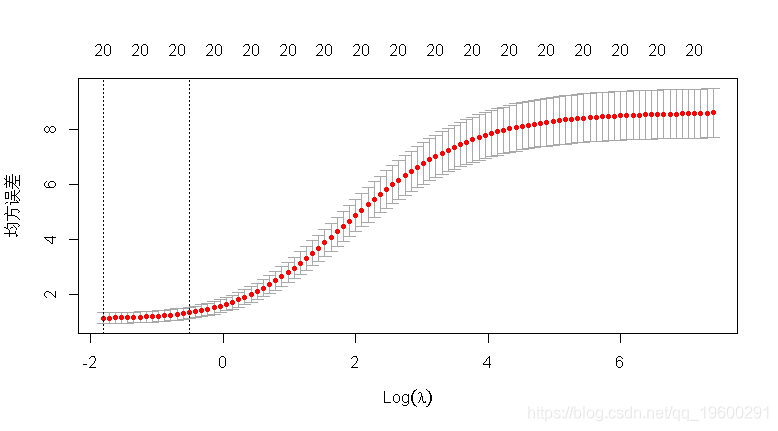
文章图片

1. ## 在误差最小λ处提取系数
2. cv$lambda.min

## [1] 0.1789759

1. ## s：需要进行预测的惩罚参数“lambda”的值 。 默认值是用于创建模型的整个序列 。
2. coef( s = lambda.min)
3. ## 21 x 1 sparse Matrix of class "dgCMatrix"
4. ## 1
5. ## (Intercept) 0.149041059
6. ## V1 1.302684272
7. ## V2 0.035835380
8. ## V3 0.719936146
9. ## V4 0.036473087
10. ## V5 -0.863490158
11. ## V6 0.605750873
12. ## V7 0.123446432
13. ## V8 0.376890626
14. ## V9 -0.040012847
15. ## V10 0.105999328
16. ## V11 0.240967604
17. ## V12 -0.066363634
18. ## V13 -0.042048935
19. ## V14 -1.092107794
20. ## V15 -0.119566353
21. ## V16 -0.035859663
22. ## V17 -0.038827463
23. ## V18 0.061785988
24. ## V19 -0.001409608
25. ## V20 -1.079879797
26. ## 截距估计应该剔除 。
27. (coef(cv, s = lambda.min))[-1]

这个初始过程给出了基于10折交叉验证选择的最佳岭回归模型的一组系数 ， 使用平方误差度量作为模型性能度量 。

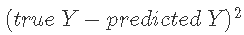
文章图片

KNNL和Hadi中提到的另一种选择lambda的方法是选择最小的lambda ， 这样系数的轨迹是稳定的 ， VIF变得足够小 。 在这种情况下 ， VIF的定义必须包括惩罚因子lambda ， 这在Hadi的p295和knll的p436中有说明 。

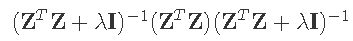
文章图片

是标准化的协变量矩阵. 是原始非标准化协变量的相关矩阵 . 该计算可定义如下 。

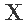
文章图片


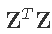
文章图片


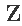
文章图片

1. vif <- function(x, lambda) {
2. ZtZ <- cor(x)
3. diag(solve(ZtZ + lambdaI %*% ZtZ %*% solve(ZtZ + lambdaI)
5. ##
6. ggplot(mapping = aes(x = lambda, y = value, group = key, color = key)) +
7. geom_line() +

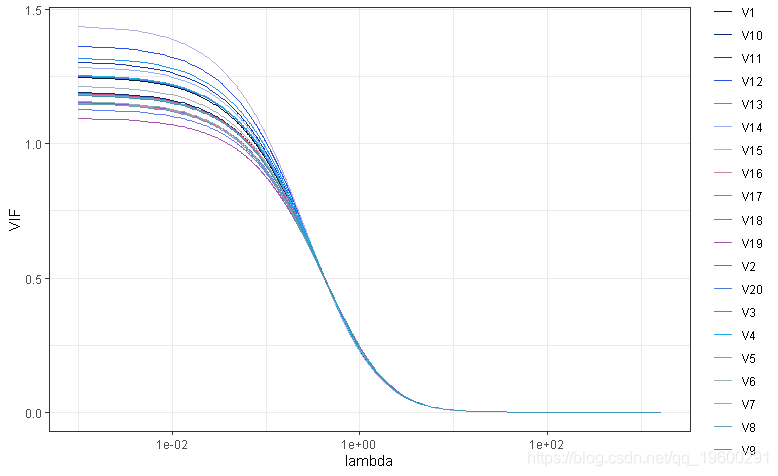
文章图片