原文链接： http://tecdat.cn/?p=21557
分段回归( piecewise regression ) ， 顾名思义 ， 回归式是“分段”拟合的 。 其灵活用于响应变量随自变量值的改变而存在多种响应状态的情况 ， 二者间难以通过一种回归模型预测或解释时 ， 不妨根据响应状态找到合适的断点位置 ， 然后将自变量划分为有限的区间 ， 并在不同区间内分别构建回归描述二者关系 。分段回归最简单最常见的类型就是分段线性回归( piecewise linear regression ) ， 即各分段内的局部回归均为线性回归 。
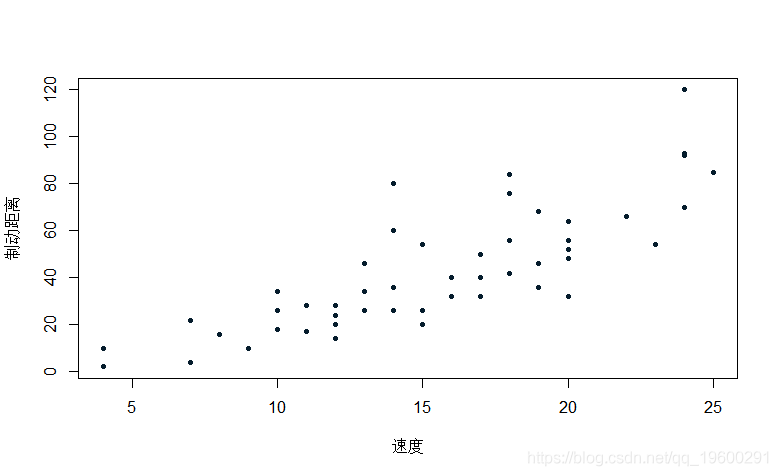
本文我们试图预测车辆的制动距离 ， 同时考虑到车辆的速度 。

1. > summary(reg)
2. Call:
3. Residuals:
4. Min 1Q Median 3Q Max
5. -29.069 -9.525 -2.272 9.215 43.201
6. Coefficients:
7. Estimate Std. Error t value Pr(>|t|)
8. (Intercept) -17.5791 6.7584 -2.601 0.0123 *
9. speed 3.9324 0.4155 9.464 1.49e-12 ***
10. ---
11. Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
12. Residual standard error: 15.38 on 48 degrees of freedom
13. Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438
14. F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12

文章图片

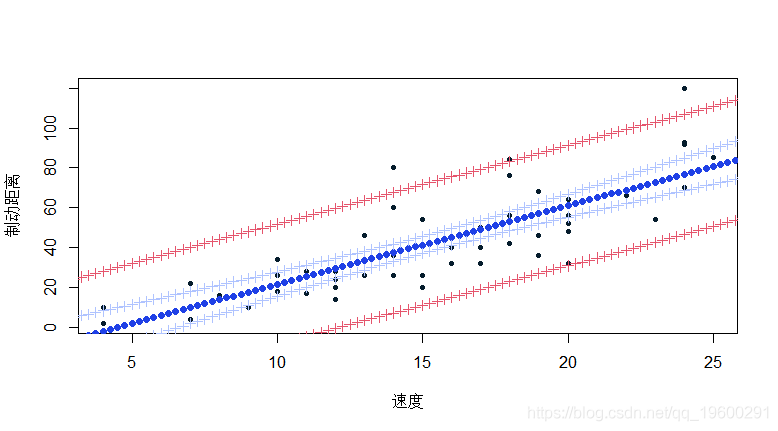
要手动进行多个预测 ， 可以使用以下代码（循环允许对多个值进行预测）

1. for(x in seq(3,30)){
2. + Yx=b0+b1*x
3. + V=vcov(reg)
4. + IC1=Yx+c(-1,+1)*1.96*sqrt(Vx)
5. + s=summary(reg)$sigma
6. + IC2=Yx+c(-1,+1)*1.96*s

文章图片

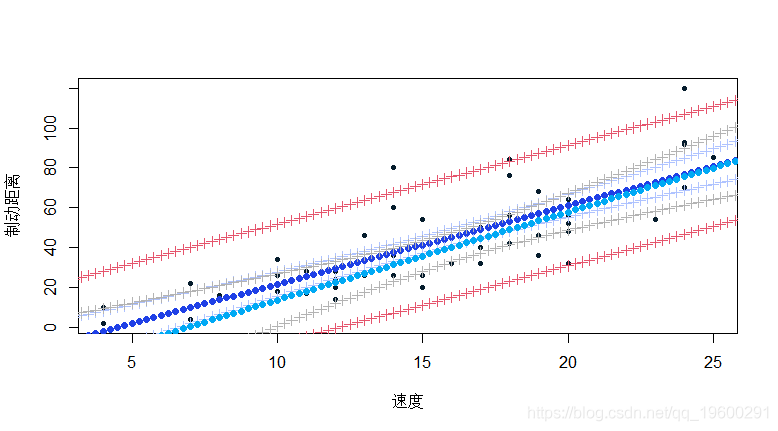
然后在一个随机选择的20个观测值的基础上进行线性回归 。
lm(dist~speed,data=https://www.sohu.com/a/cars[I,])
目的是使观测值的数量对回归质量的影响可视化 。

1. Residuals:
2. Min 1Q Median 3Q Max
3. -23.529 -7.998 -5.394 11.634 39.348
4. Coefficients:
5. Estimate Std. Error t value Pr(>|t|)
6. (Intercept) -20.7408 9.4639 -2.192 0.0418 *
7. speed 4.2247 0.6129 6.893 1.91e-06 ***
8. ---
9. Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
10. Residual standard error: 16.62 on 18 degrees of freedom
11. Multiple R-squared: 0.7252, Adjusted R-squared: 0.71
12. F-statistic: 47.51 on 1 and 18 DF, p-value: 1.91e-06
13. > for(x in seq(3,30,by=.25)){
14. + Yx=b0+b1*x
15. + V=vcov(reg)
16. + IC=Yx+c(-1,+1)*1.96*sqrt(Vx)
17. + points(x,Yx,pch=19

文章图片

可以使用R函数进行预测 ， 具有置信区间

1. fit lwr upr
2. 1 42.62976 34.75450 50.50502
3. 2 84.87677 68.92746 100.82607
4. > predict(reg,
5. fit lwr upr
6. 1 42.62976 6.836077 78.42344

当有多个解释变量时 ， “可视化”回归就变得更加复杂了

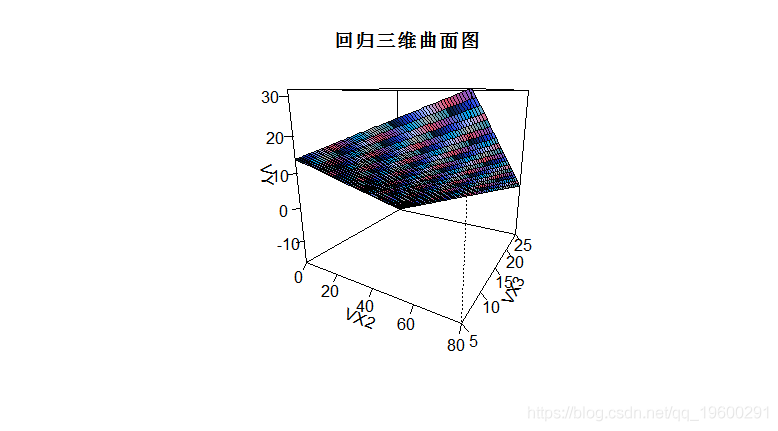
1. > image(VX2,VX3,VY)
2. > contour(VX2,VX3,VY,add=TRUE)

这是一个回归三维曲面图
> persp(VX2,VX3,VY,ticktype=detailed)

文章图片

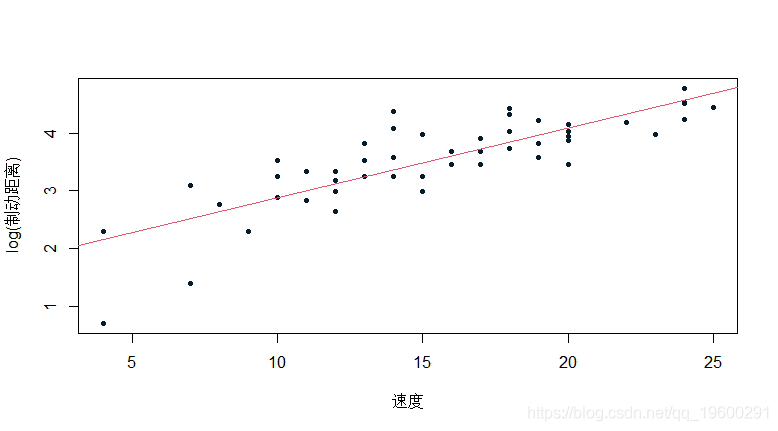
我们将更详细地讨论这一点 ， 但从这个线性模型中可以很容易地进行非线性回归 。 我们从距离对数的线性模型开始

1. > abline(reg1)

文章图片

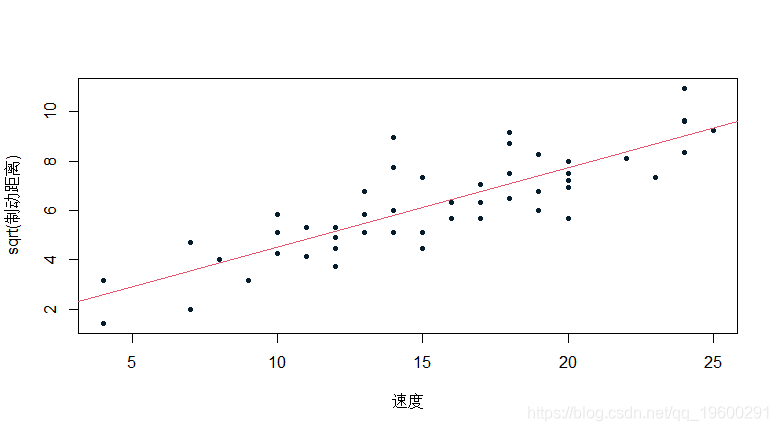
因为我们在这里没有任何关于距离的预测 ， 只是关于它的对数......但我们稍后会讨论它
lm(sqrt(dist)~speed,data=https://www.sohu.com/a/cars)