例如：在平面直角坐标系中画出y=-3x+4的图象 。
简析：很显然 ， b=4 ， 即为图象与y轴交点的纵坐标 ， 所以再确定一个点即可 ， 不妨令x=1 ， 则y=1 。 所以过（0 ， b),(1,1)画直线即可 。
解析式的求法：
由于一次函数的解析式为：y=kx+b 。 除了两个变量y与x外 ， 还有两个常数k和b ， 要想求出两个未知数的值 ， 则至少要利用两个点的坐标 。
例如：一条直线 ， 经过点（3 ， 2）和（-1 ， 5） ， 试求其表达式 。
解：设其解析式为y=kx+b
则2=3k+b（1）；5=-k+b（2）
由（1）（2）即可求出k与b的值了 ， 不再赘述 。
知识点：
k的绝对值的大小决定着图象的倾斜程度 ， 当k的绝对值越大时 ， 离y轴越近 ， 即直线与y轴夹角越小；k的绝对值越小 ， 离y轴越远 ， 即与y轴夹角越大 。
如果两个一次函数中的k相等 ， 那么说明这两条直线倾斜度一样 ， 例如：y=2x-3与y=2x+9 ， 倾斜度是一样的 ， 由于图象分别在y轴的负半轴和正半轴 ， 故两直线平行 。
对于两个一次函数：k的值相同 ， b的值也相同时 ， 两直线重合；k的值相同 ， b的值不同时 ， 两直线平行；k的值不相同时 ， 则两直线相交 。
定义域 ， 值域
【函数入门基础知识,excel函数入门基础知识】

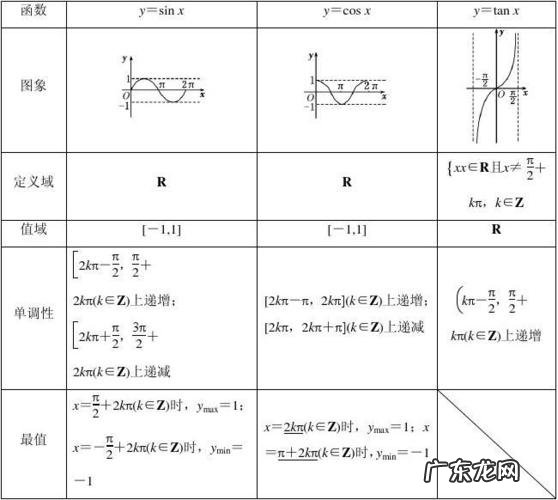
函数的基本知识

• 函数奇偶性的判断口诀,函数运算奇偶性的判断口诀
• excel做文档函数怎么做
• 美甲新手入门教程修指甲 你学会了吗
• 在健身前，你觉得需不需要学习健身方面的基础知识，类似于指南之类的？为什么？
• 儿童初学溜冰入门技巧
• 人工三怎么玩高难度动作 人工少女3入门攻略
• 学数控刚入门需要先学什么?
• 单反摄影入门教程 7个技巧
• 新手淘宝开店入门基础知识分享，有哪些需要做好?
• 提高外卖人员的准入门槛 在餐盒里小便外卖员被拘留14天