【椭圆体的表面积公式 椭圆面积计算】阿基米德在他的著作《关于圆锥体和球体》中计算了一个椭圆的面积(命题4) 。
当我们垂直地缩小一个圆时，我们得到一个椭圆 。椭圆有一条长半轴和一条短半轴 。

文章插图


文章插图

椭圆面积的公式是对圆面积的一种美丽的推广 。长半轴a、短半轴b的椭圆面积为:

文章插图

首先，我们用直观的方法推导出这个公式 。但阿基米德的“方法”和严格的定理证明之间有明显的区别 。
之后，我们将解释阿基米德是如何证明这个结果的 。
在椭圆周围半径为a的圆称为它的辅助圆 。如果我们(垂直地)缩小这个圆，我们得到一个椭圆 。给定椭圆上的点m，它满足关系式:

文章插图

阿基米德考虑了椭圆和辅助圆内接的一些多边形 。这些多边形的边数等于4的倍数，并以水平直径的相对端点作为顶点 。
圆内接的多边形P\'是正多边形，P是内接在椭圆E上的多边形，其顶点是从P\'的顶点到E的水平轴的垂线与椭圆E的交点，我们具有以下关系

文章插图

那么两个多边形P和P\'的面积关系是：

文章插图

但是这些多边形可以有任意多的边，它们可以无限的趋近圆和椭圆

文章插图

我们得到椭圆面积的公式:

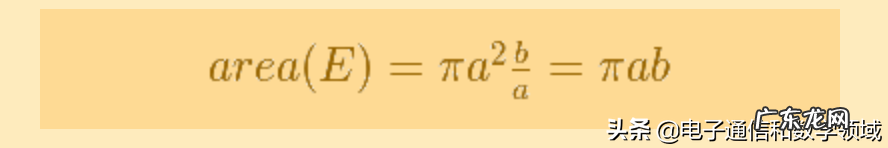
文章插图

如果我们的直觉是正确的，那么这就是椭圆面积的公式 。使用mathlet缩放，我们可以看到非常好的近似值，但多边形永远不会完全填充整个椭圆或圆

文章插图

这是一个很好的方法，但阿基米德需要一个逻辑严密的证明 。

• 请问我只吃素，从小的生活习惯，一点肉腥不吃，为什么还会胖，这样的我该怎么减肥？
• 端午节历史渊源从哪开始？端午节最有名的古诗有哪些诗句？
• 读书的最大意义是什么？
• 高铁学校有哪些 学高铁的学校
• 力的三要素是指力的那三要素 力的三要素是哪三个
• 互联网大会为什么会选择桐乡乌镇这个跟互联网很难搭上边的小镇？
• 例如：耐克 请问你现在还会买前段时间遭受抵制的品牌相关产品吗？理由是什么？
• 脸字开头的成语大全集 脸开头的成语有哪些
• 航天员在太空起床洗漱的画面 神十三航天员起床洗漱画面曝光
• 并非成本过高而是一种低成本的策略 钟南山中国防疫政策并非成本过高