矢量的求导公式矢量求导的基本运算法则为 _现在

小编现在给大家详细介绍关于“矢量求导的基本运算法则为”的核心内容以及“矢量的求导公式”的相关知识，希望能够帮到您。
如图，做圆周运动位置矢量关于时间求导，为什么是速度矢量啊？

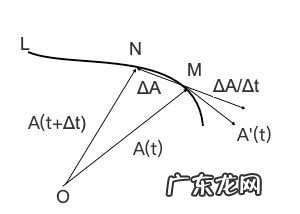
文章插图

运动位置矢量不就是位移么，位移对时间求导就是速度啊，当△s和△t趋近于o ，速度就是切线方向了
矢量的一阶求导是否有意义相关试题【1】
矢量函数导数r'（t）等于零表示什么
那么在这点的几何意义呢？就是高数中求切矢法矢都要求不为0 ，但是为零时几何图形又如何呢如果r是位移,则会矢量函数导数r'（t）表示这个时刻的瞬时速度,等于0表示瞬时速度为0相关试题【2】
一个概念细节问题：矢量（向量）求导
力学里面定义,速度是位矢对时间的一阶导数,即v=dr/dt（v和r加黑加粗).而速度和位矢都是矢量,时间是标量,请问矢量也可以像标量、像数那样求导（对标量）?如果可以,怎样求导呢?是否将矢量当做标量那样处理,即标量所成立的求导法则矢量也成立?设位置向量S（t）＝（x（t）,y（t）,z（t））,
则：速度向量V（t）
＝d[S（t）]/dt＝（d（x（t））/dt,d（y（t））/dt,d（z（t））/dt）
加速度向量A（t）
＝d2[S（t）]/dt2
＝（d2（x（t））/dt2,d2（y（t））/dt2,d2（z（t））/dt2）
[向量求导,全部由分量（标量）求导来完成.]相关试题【3】
对于第一点,矢量的导数应该还是矢量,但是在直角坐标系中,单位矢量的导数为什么不是矢量而是一个数：0因为单位导数是常量,所以导数是0,不过不是数0,而是零矢量,但是反正多项式中的所有单项式肯定是一样阶的,所以矢量0加的肯定是矢量,不会是其他的东西,所以可以直接把矢量0和数量0还有零矩阵之类全当成0来看,不需要区分.方向导数是矢量还是标量
f(x ， y)在点P(x0 ， y0)沿方向l的方向导数为一固定数值，不是矢量单位矢量对时间t的导数是多少
1、如果是直角坐标系的是单位矢量i、j、k,因为它们是常矢量,导数等于0；
2、如果是物理问题中的任意点所在处的力、强度、、、等单位矢量,
由于这个单位矢量在空间的取向不固定,只要空间各点的物理量随时间变化,
单位矢量的导数就不等于0了.具体计算如下：
A、由于物理中的单位矢量的实质是：(位置矢量) 除以 (位置矢量的模),
所以,求导数时,是一个商的求导,其中的分子有两部份组成；
B、分子中的第一项涉及的是d(位置矢量r)/dt,这是切向速度矢量；
C、分子中的第二项涉及大是dr/dt,这是径向速率标量,但要乘以位置矢量；
D、C中的速率标量乘以位置矢量再除以位置矢量的模,就是径向速度,而其中被除的
矢量求导是哪个课程里讲的矢量分析。
在物理学中，很多定义都跟矢量有关，请问瞬时速度是位置矢量对时间的导数，一个矢量如何求导用二维空间举个例子， v（矢量）=a(t)i（矢量）+b(t)j（矢量）， i和j分别为两个基矢（或者你理解为分别是沿x,y正方向的单位矢量就好），那么这里的a(t)和b(t)就是关于t的标量函数。对他们分别求导再分别乘i和j矢量就好。
本质上还是采用了正交分解的方法。
希望可以帮到你
没有学过矢量求导，想知道这个物理公式是怎么来的。这个式子就是速度的微分就是加速度。速度的在一点的斜率就是加速度
【矢量的求导公式矢量求导的基本运算法则为】以上内容就是关于矢量求导的基本运算法则为和矢量的求导公式的全部内容，是由小编认真整理编辑的，如果对您有帮助请收藏转发...感谢支持！

特别声明：本站内容均来自网友提供或互联网，仅供参考，请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系，我们将在24小时内删除。

矢量的求导公式 矢量求导的基本运算法则为

矢量的求导公式矢量求导的基本运算法则为