抽屉原理的诀窍,抽屉原理的公式【详细点 _抽屉

小学奥数关于抽屉原理的知识点讲解【 #小学奥数# 导语】数学给予人们的不仅是知识，更重要的是能力，这种能力包括观察实验、收集信息、归纳类比、直觉判断、逻辑推理、建立模型和精确计算。这些能力和培养，将使人终身受益。以下是整理的相关资料，希望对您有所帮助。
【抽屉原理的诀窍,抽屉原理的公式【详细点】抽屉原理
抽屉原则一：如果把（n+1）个物体放在n个抽屉里，那么必有一个抽屉中至少放有2个物体。
例：把4个物体放在3个抽屉里，也就是把4分解成三个整数的和，那么就有以下四种情况：
①4=4+0+0②4=3+1+0③4=2+2+0④4=2+1+1
观察上面四种放物体的方式，我们会发现一个共同特点：总有那么一个抽屉里有2个或多于2个物体，也就是说必有一个抽屉中至少放有2个物体。
抽屉原则二：如果把n个物体放在m个抽屉里，其中n>m，那么必有一个抽屉至少有：
①k=[n/m]+1个物体：当n不能被m整除时。
②k=n/m个物体：当n能被m整除时。
理解知识点：[X]表示不超过X的整数。
例[4.351]=4；[0.321]=0；[2.9999]=2；
关键问题：构造物体和抽屉。也就是找到代表物体和抽屉的量，而后依据抽屉原则进行运算。
1、有红、黄、蓝、绿四种颜色小旗各一面，取其中一面小旗，或者多面小旗由上而下挂在旗杆上作为信号（挂多面小旗时，不同顺序表示不同信号，如：挂出红、黄颜色小旗时，顺序为红黄与顺序为黄红表示不同的信号）。问：一共有（）多少种信号？如果某天一共发出信号323次，那么这一天必定出现某种相同的信号至少有（）次？
2、一副*牌一共有54张，最少要抽取几张牌，方能保证其中至少有2张牌有相同的点数？
3、自制的一副玩具牌一共计52张（含有四种颜色的牌：红桃、红方、黑桃、黑梅。每种牌都有1点、2点….13点）。洗好后背面朝上放好，一次至少抽取几张牌，才能保证其中必定有2张牌点数和颜色都相同。如果要求一次抽出的牌中必定有3张牌的点数是相邻的（不计颜色的），那么至少需要取多少张牌？
4、在8*8的方格纸中，每个方格内可以填上1-4四个自然数中的任意一个，填满以后，对每个2%2的田字形内的4个自然数求和。在这些和中，相同的和至少有（）多少个？（*在此代表乘号）
5、用数字1、2、3、4、5、6填满一个6*6的方格表，如图所示，每个小方格中只填写其中的一个数字。将其中2*2正方形内的四个数字的和称为这个2*2正方形的标示数。问能否给出一种填法，使得任意两个标示数均不相同？如果能，请举出一个例子？不能则请说明理由？（*在此代表乘号）（图请根据题意自己画，不是太难。）
6、两条直线相交，四个交角中的一个锐角或一个直角称为这两条直线的夹角。现在平面上有若干条直线，他们两两相交，并且夹角只能是30度、60度或者90度。问：至少有多少条直线？
7、雪帆学校有55个学生参加数学竞赛，已知将参赛人任意分成四组，则必有一组女生多于2人，又知道参赛者中任何10人中必有男生。则参赛男生的人数为（）人？
8、王跃老师带着若干个小朋友去购买单价为3元和5元的两种商品，每个小朋友至少买一件，但是每个人购买商品的总金额不得超过15元，王跃老师说，小朋友中一定至少有三人购买的两种商品的数量是完全相同的。问：至少有多少名小朋友？
9、雪帆奥数辅导班有10名优秀少先队员，同学们送花给他们，要使得他们中至少有两人的得到的花的数量是相同的，那么至少需要准备多少朵花？
10、五一班的同学要从10名候选人里面投票选择班干部。如果每个同学只要投票选择两名候选人，那么这个班级至少应该有多少个同学，才能保证必有两个或者两个以上的同学投相同的两名两名候选人的票？

文章插图
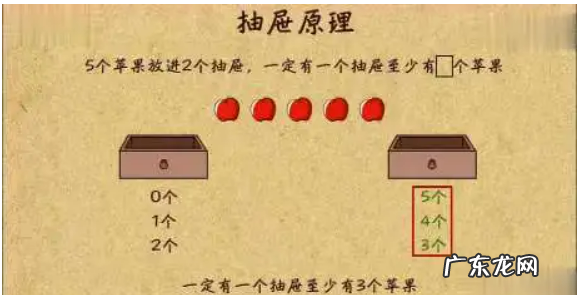
抽屉原理的三个公式小学1、三个苹果放进两个抽屉，必有一个抽屉里至少有两个苹果。
2、抽屉原则的常见形式一，把n+k（k≥1）个物体以任意方式全部放入n个抽屉中，一定存在一个抽屉中至少有两个物体。
3、二，把mn+k（k≥1）个物体以任意方式全部放入n个抽屉中，一定存在一个抽屉中至少有m+1个物体。
4、三，把m1+m2+…+mn+k（k≥1）个物体以任意方式全部放入n个抽屉中，那么后在一个抽屉里至少放入了m1+1个物体，或在第二个抽屉里至少放入了m2+1个物体，…… ，或在第n个抽屉里至少放入了mn+1个物体四，把m个物体以任意方式全部放入n个抽屉中，有两种情况：①当n|m时（n|m表示n整除m），一定存在一个抽屉中至少放入了个物体；②当n不能整除m时，一定存在一个抽屉中至少放入了[ ]+1个物体（[x]表示不超过x的最大整数）。

文章插图
抽屉原理的三个公式讲解原理1：把多于n+1个的物体放到n个抽屉里，则至少有一个抽屉里的东西不少于两件。
第二抽屉原理
把（mn－1）个物体放入n个抽屉中，其中必有一个抽屉中至多有（m—1）个物体(例如，将3×5-1=14个物体放入5个抽屉中，则必定有一个抽屉中的物体数少于等于3-1=2) 。

文章插图
扩展资料
在任意的五个自然数中，是否其中必有三个数的和是3的倍数。
分析与解：根据例2的讨论，任何整数除以3的余数只能是0，1，2 。现在，对于任意的五个自然数，根据抽屉原理，至少有一个抽屉里有两个或两个以上的数，于是可分下面两种情形来加以讨论。
第一种情形。有三个数在同一个抽屉里，即这三个数除以3后具有相同的余数。因为这三个数的余数之和是其中一个余数的3倍，故能被3整除，所以这三个数之和能被3整除。
第二种情形。至多有两个数在同一个抽屉里，那么每个抽屉里都有数，在每个抽屉里各取一个数，这三个数被3除的余数分别为0，1，2 。因此这三个数之和能被3整除。
综上所述，在任意的五个自然数中，其中必有三个数的和是3的倍数。
抽屉原理的诀窍构造运用抽屉原理的一般步骤是：根据元素特征，构造抽屉、把元素放入抽屉。将多于N件的物品任意放入N个抽屉里，则至少有一个抽屉里的物品数不少于2（至少有2件物品在同一个抽屉里）。

文章插图
将多于n件的物品任意放入n个抽屉里，则至少有一个抽屉里的物品数不少于2（至少有2件物品在同一个抽屉里）。举例，买了6块（也可以是7块8块）糖，要放在5个小糖匣子里，不管你怎么放，至少有个一个匣子里的糖数不少于2 。运用抽屉原理的一般步骤是：根据元素特征，构造抽屉、把元素放入抽屉。

文章插图

特别声明：本站内容均来自网友提供或互联网，仅供参考，请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系，我们将在24小时内删除。