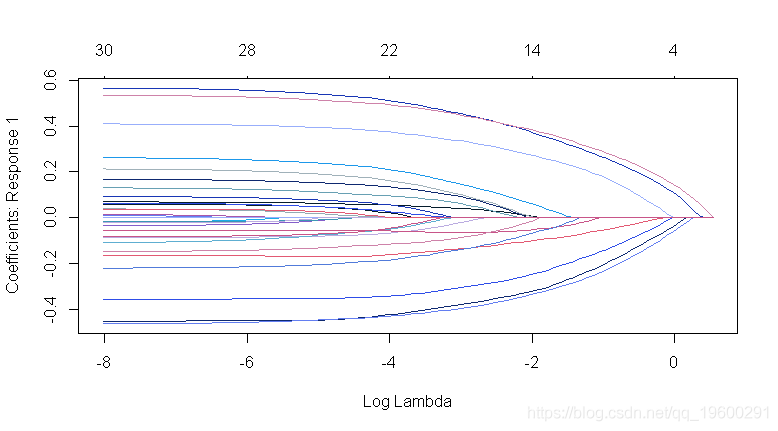
模型|拓端tecdat|R语言自适应LASSO 多项式回归、二元逻辑回归和岭回归应用分析( 四 ) 多项式|lambda|语言|cv|alpha|惩罚

## V19 0.090783173 -0.147044947 0.056261774

## V20 -0.010749594 0.146821172 -0.136071578

## V21 0.059468598 -0.008259112 -0.051209485

## V22 0.133514075 -0.030352819 -0.103161256

## V23 0.070174614 -0.054781769 -0.015392844

## V24 0.027344225 0.164797661 -0.192141886

## V25 0.010677968 0.014023080 -0.024701049

## V26 0.010490474 -0.034644559 0.024154085

## V27 -0.008201249 0.114562955 -0.106361705

## V28 -0.115249536 -0.067581191 0.182830727

## V29 0.027760120 0.056857406 -0.084617526

## V30 -0.062642211 -0.007339614 0.069981825

## 转换为矩阵

## 截距估计应该取消。

1 / abs(as.matrix(best_ridge_coef2)[-1,])

## 1 1 1

## V1 17.619846 3.003574 3.620794

## V2 3.023239 7.381929 2.144832

## V3 2.396282 5.989675 3.994260

## V4 3.634942 13.168687 2.848635

## V5 2.783104 2.235542 11.362639

## V6 3.139810 23.655569 3.620339

## V7 14.450127 9.627043 28.842957

## V8 2.509836 17.712347 2.198333

## V9 9.913386 1.202684 1.072562

## V10 12.592946 1.816643 2.122889

## V11 64.353133 43.721407 26.033972

## V12 42.764219 26.761045 16.460422

## V13 6.155483 3.688727 9.204764

## V14 5.776046 7.827282 22.040732

## V15 33.957479 28.069106 161.870875

## V16 12.798253 15.070757 84.875262

## V17 6.908278 7.248456 147.200381

## V18 30.368044 14.030089 9.596493

## V19 11.015257 6.800642 17.774057

## V20 93.026766 6.811007 7.349073

## V21 16.815597 121.078385 19.527632

## V22 7.489847 32.945869 9.693562

## V23 14.250167 18.254248 64.965251

## V24 36.570794 6.068047 5.204487

## V25 93.650773 71.311008 40.484111

## V26 95.324582 28.864561 41.400864

## V27 121.932644 8.728825 9.401880

## V28 8.676825 14.797016 5.469540

## V29 36.022899 17.587858 11.817883

## V30 15.963677 136.246945 14.289424

## 执行自适应套索

## 多项式回归

family = "multinomial",

## ‘alpha = 1’ 是套索惩罚， 'alpha=0'是岭惩罚。

alpha = 1,

## 惩罚系数：可以对每个系数应用单独的惩罚因子。这是一个乘以“lambda”以允许差异收缩的数字。对于某些变量可以为0 ，这意味着没有收缩，并且该变量始终包含在模型中。对于所有变量，默认值为1（对于“exclude”中列出的变量，默认值为无限大）。注意：惩罚因子在内部被重新调整为与nvars相加， lambda序列将反映这种变化。

模型|拓端tecdat|R语言自适应LASSO 多项式回归、二元逻辑回归和岭回归应用分析

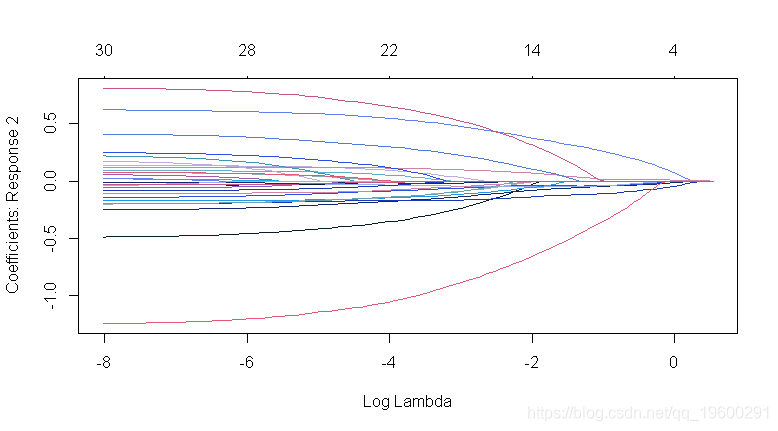
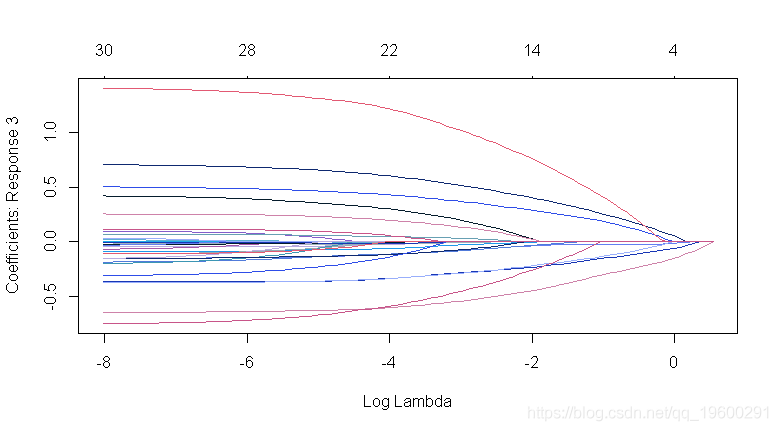
文章图片

## 使用10折CV执行自适应套索
## 类型。度量:用于交叉验证的损失。
type.measure = "偏差",
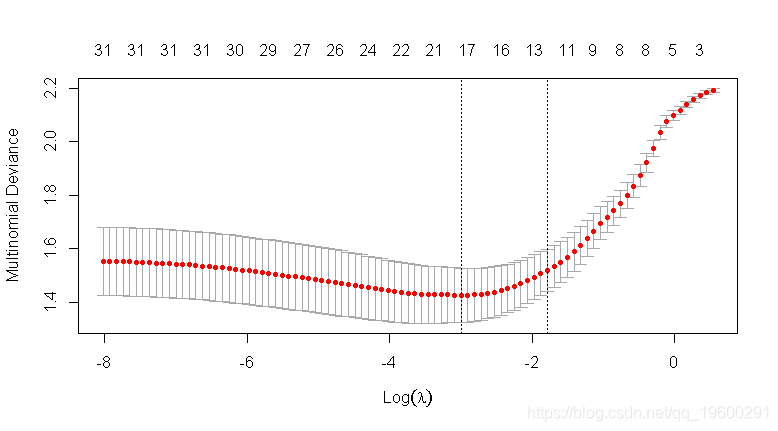
## 惩罚vs CV MSE图
plot(alasso2_cv)

文章图片

## 在误差最小λ处提取系数
lambda.min

## [1] 0.023834

## s：需要进行预测的惩罚参数“lambda”的值。默认值是用于创建模型的整个序列。
do.call(cbind, coef(alasso2_cv, s = lambda.min))
## 31 x 3 sparse Matrix of class "dgCMatrix"
## 1 1 1
## (Intercept) 0.001070916 0.029687114 -0.030758030
## V1 0.051853991 -0.329785101 0.277931110
## V2 -0.414609162 -0.166765504 0.581374666
## V3 0.498638681 -0.172468859 -0.326169822
## V4 -0.336005338 -0.079578260 0.415583598
## V5 -0.424216967 0.532071434 -0.107854467
- 上一页
- 1
- 2
- 3
- 4
- 5
- 6
- 下一页
特别声明：本站内容均来自网友提供或互联网，仅供参考，请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系，我们将在24小时内删除。