自适应LASSO ## 执行自适应LASSO glmnet(x = y = ## 类型 。 度量:用于交叉验证的损失 。 ##“alpha=1”是套索惩罚 ， “alpha=0”是岭惩罚 。 alpha = 1, ## ## 惩罚系数：...

自适应LASSO

1. ## 执行自适应LASSO
2. glmnet(x = y =
3. ## 类型 。 度量:用于交叉验证的损失 。
4. ##“alpha=1”是套索惩罚 ， “alpha=0”是岭惩罚 。
5. alpha = 1,
6. ##
7. ## 惩罚系数：可以对每个系数应用单独的惩罚因子 。 这是一个乘以“lambda”以允许差异收缩的数字 。 对于某些变量可以是0 ，这意味着没有收缩 ， 而且这个变量总是包含在模型中 。 对于所有变量 ， 默认值为1（对于“exclude”中列出的变量 ， 默认值为无限大） 。 注意：惩罚因子在内部被重新调整为与nvars相加 ， lambda序列将反映这种变化 。

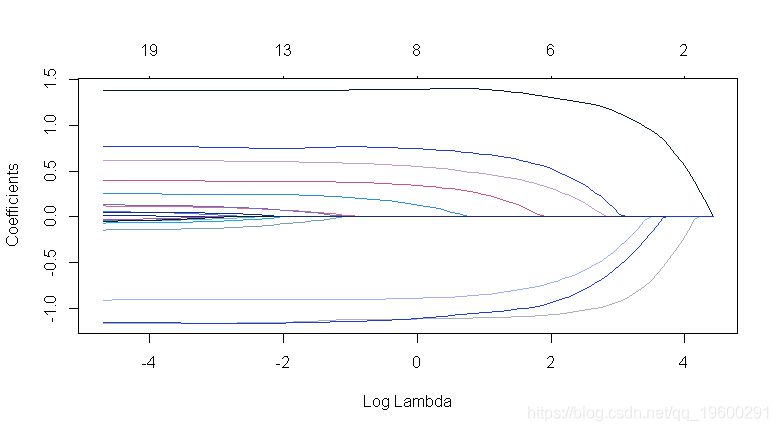
文章图片

1. ## 使用10折CV执行自适应套索
2. ## 类型 。 度量:用于交叉验证的损失 。
3. 类型 。 测量= " mse ",
4. ## K = 10 是默认值 。
5. nfold = 10,
6. ## ‘alpha = 1’ 是套索惩罚 ， 'alpha=0'是岭惩罚 。
7. ##
8. ## 惩罚系数：可以对每个系数应用单独的惩罚因子 。 这是一个乘以“lambda”以允许差异收缩的数字 。 对于某些变量可以为0 ， 这意味着没有收缩 ， 并且该变量始终包含在模型中 。 对于所有变量 ， 默认值为1（对于“exclude”中列出的变量 ， 默认值为无限大） 。 注意：惩罚因子在内部被重新调整为与nvars相加 ， lambda序列将反映这种变化 。
9. ## 惩罚vs CV MSE图

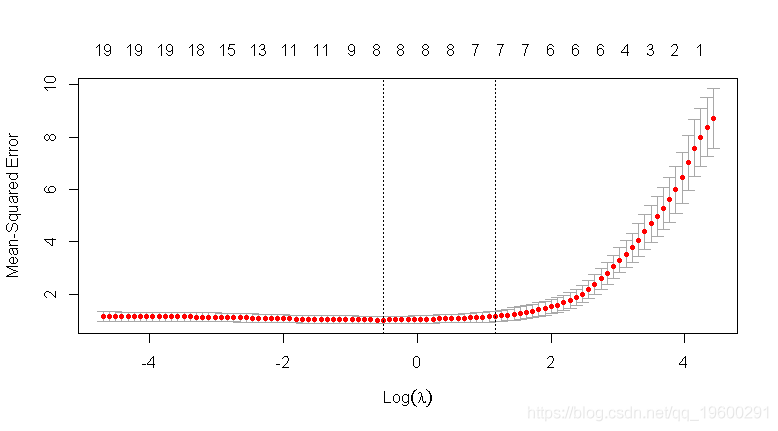
文章图片

1. ## 在误差最小λ处提取系数
2. lambda.min

## [1] 0.7193664

1. ## s：需要进行预测的惩罚参数“lambda”的值 。 默认值是用于创建模型的整个序列 。
2. best_alasso_coef1
3. ## 21 x 1 sparse Matrix of class "dgCMatrix"
4. ## 1
5. ## (Intercept) 0.1269539
6. ## V1 1.3863728
7. ## V2 .
8. ## V3 0.7573538
9. ## V4 .
10. ## V5 -0.8937983
11. ## V6 0.5718800
12. ## V7 .
13. ## V8 0.3654255
14. ## V9 .
15. ## V10 .
16. ## V11 0.1824140
17. ## V12 .
18. ## V13 .
19. ## V14 -1.1150736
20. ## V15 .
21. ## V16 .
22. ## V17 .
23. ## V18 .
24. ## V19 .
25. ## V20 -1.1268794

那个惩罚系数参数允许指定系数特定的惩罚级别 。 这里我们使用自适应LASSO惩罚 ， 即最佳岭系数绝对值的逆 。
最终模型Rsquare

1. ## R^2函数
2. ## https://en.wikipedia.org/wiki/Coefficient_of_determination
3. ## 总SS
4. ss_tot <- sum((y - ybar)^2)
5. ## 剩余 SS
6. ss_res <- sum((y - yhat)^2)
7. ## R^2 = 1 - ss_res/ ss_tot
8. ## 调整R^2函数
9. ## n个样本 ， p个参数
10. ## 获取 R^2
11. r_sq(as.vector(y_cont), as.vector(predict(alasso1, newx =

## [1] 0.906806

1. ##获得调整R ^ 2
2. adj_r_sq(r_squared_alasso1, n = nrow(y_cont),

## [1] 0.9007934

1. ## 交叉验证测试集R^2
2. ## alasso1_cv$cvm[1] 是截距模型的交叉验证测试集均方误差 。
3. 1 - cvm[lambda == lambda.min] / cvm[1]

## [1] 0.8854662
交叉验证测试集Rsquare

1. lapply(unique( foldid), function(id) {
2. ## 拟合排除测试集 (foldid == id)
3. glmnet(x = x_cont[alasso1_cv$foldid != id,],
4. y = y_cont[alasso1_cv$foldid != id],
5. ## 使用模型拟合最佳lambda测试集Y?hat
6. predict(fit, newx = x_cont[alasso1_cv$foldid == id,],
7. ## 测试组 R^2
8. 1 - sum((y - y_pred)^2) / sum((y - mean(y))^2)
9. }) %>%
10. ## [1] 0.8197796 0.9090972 0.9499495 0.8019303 0.8637534 0.7184797 0.8579943 0.9250376 0.8300891
11. ## [10] 0.9188004

## [1] 0.8594911
多项式例子